2023年 国家一般職(高卒 技術) No.65 土木基礎力学　解説

　問 題　　　　　

水平に置かれた内径 1 m、水路長 50 m の円形管水路において、流量が 0.3 m³/s で水が流れているとき、摩擦損失水頭として最も妥当なのはどれか。ただし、重力加速度の大きさを10 m/s²、円形管の摩擦損失係数を 0.05、円周率を 3 とする。

1．0.002 m
2．0.004 m
3．0.008 m
4．0.02 m
5．0.04 m　

 

 

 

 

 

　解 説　　　　　

【摩擦損失水頭の基礎知識】
水頭とは、水の持つエネルギーを水柱の高さとして表したもの　のことです。エネルギーが位置エネルギーや運動エネルギーに分けられるように、水頭も位置水頭などに分けられます。摩擦損失水頭とは、摩擦によって失われるエネルギーのことと考えればよいです。

「円管での摩擦損失水頭」は公式です。
管の長さに比例するのはなんとなくイメージでわかるのではないでしょうか。また、管が広いとスムーズに流れて損失が少ないことを反映して、直径に反比例します。管の長さを l、直径を d とします。また、以降 f を摩擦損失係数と呼びます。

水頭が head なので 摩擦損失水頭を ΔH とすると ΔH = f × l/d × v²/2g です。「v²/2g」は、ベルヌーイの定理における、運動エネルギー部分と対応している点を意識すると覚えやすいと思います。

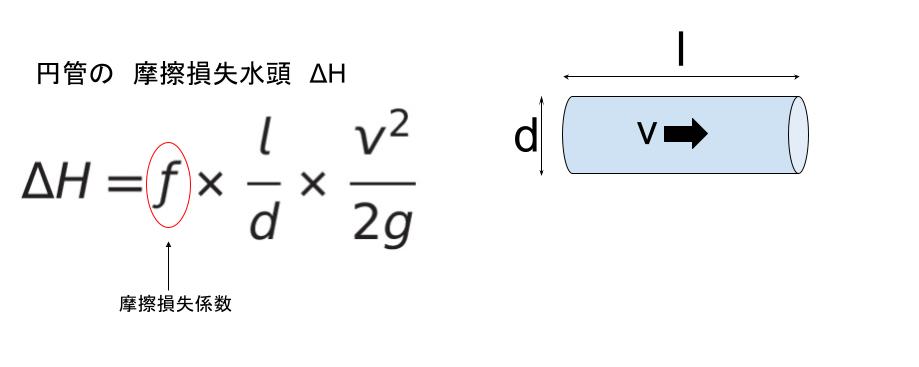
問題文より
d = 1、l = 50、g = 10、f = 0.05 です。後は v がわかればよいです。流量 Q が 0.3 と与えられているので連続の式 Q = Av を思い出します。断面積 A は直径 1 m より 半径 0.5m の円の面積で、円周率は３と与えられているため、(0.5)² × 3 = 0.75 です。従って、連続の式より 0.3 = 0.75 × v  ∴ v = 0.4 です。

ΔH = 0.05 × 50/1 × (0.4)²/(2×10)
= 0.02　です。

以上より、正解は 4 です。