問 題
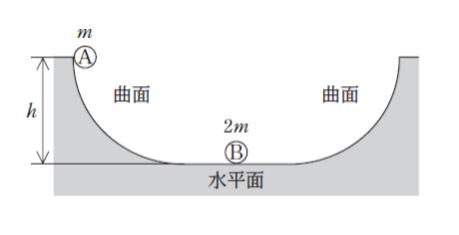
図のように、二つの曲面と水平面で構成される滑らかな面上において、水平面から高さ h の曲面上の点より質量 m の小球 A を静かに放したところ、A は、曲面を滑り、水平面上で静止している質量 2m の小球 B に衝突して一体となって運動した。このとき、一体となった A と B が達する水平面からの高さの最大値として最も妥当なのはどれか。
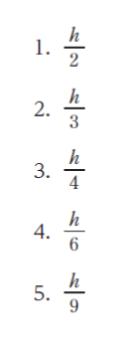
解 説
力学的エネルギーに注目すると、A が B に衝突する直前の A の速さがわかります。その後衝突して一体となった物体の速さは運動量保存則で計算できます。ある速さの物がどこまで上がっていくかは、もう一度力学的エネルギーに注目することでわかります。
【小球 A が B に衝突する直前の速さ】
力学的エネルギーは、位置エネルギー + 運動エネルギーです。滑らかな斜面なので力学的エネルギーは変化しません。これは基礎知識です。
小球 A の初期状態において、重力による位置エネルギー U = mgh です。速度は 0 なので運動エネルギー K = mv2/2 = 0 です。力学的エネルギーは U + K = mgh です。
小球 A が B に衝突する直前の 力学的エネルギーも mgh です。重力による位置エネルギー U = 0 です。従って、運動エネルギー K = mv2/2 = mgh が成立します。∴v = √2gh です。
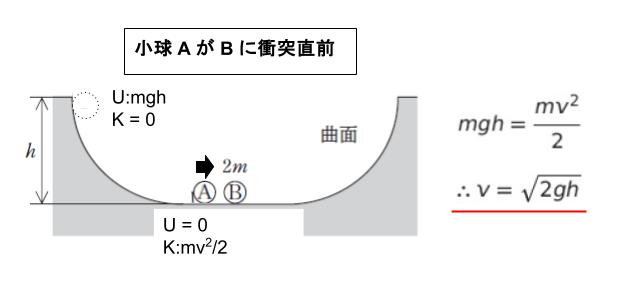
【小球 A と 小球 B の衝突前後】
衝突前後で運動量が保存されます。衝突前の運動量は、小球 A の運動量 mv = √2mgh です。
衝突後は一体となるので、質量が (m + 2m) = 3m です。衝突後の速さを v’ とおけば、運動量保存則より √2mgh = 3mv’ です。∴v’ = √2gh/3 です。
【一体となった物体のその後】
一体となった物体の運動エネルギーは
3m × (√2gh/3)2/2 = mgh/3 です。
一体となった物体が斜面を登っていき速度が 0 になった時点において、地面からの高さを h’ とおけば位置エネルギー U = 3mgh’ = mgh/3 です。従って、h’ = h/9 とわかります。
以上より、正解は 5 です。

コメント