問 題
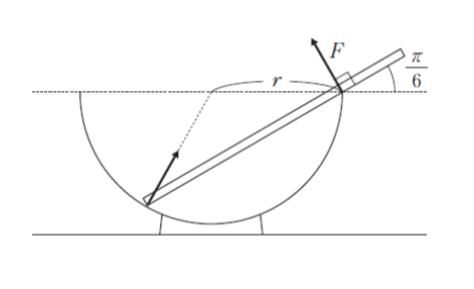
図のように、縁が水平になるように固定された半径 r の半球面上で、質量 m の一様な細い剛体棒が静止している。剛体棒と水平面のなす角が π/6 であるとき、剛体棒が半球面の縁から受ける力 F の大きさとして最も妥当なのはどれか。
ただし、重力加速度の大きさを g とし、摩擦はないものとする。なお、図中の矢印は、剛体棒が半球面から受ける力の向きを示す。
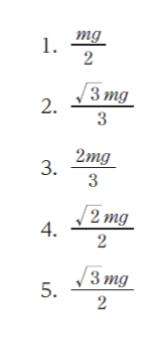
正解 (2)
解 説
・質量 m の物には、下向き mg の力が重心に作用します。
・静止時、縦の力の和 = 横の力の和 = モーメントの和 = 0 です。
棒が斜めになっているので
「縦」とは棒に垂直な力、「横」とは棒に平行な力と考えます。
お椀の底と棒が接している点を A、棒の重心を O、お椀のふちと接している点を B とします。棒の重心から下向きに mg の力が作用します。mg の力を本問における「縦」「横」に分解した図が、以下のようになります。
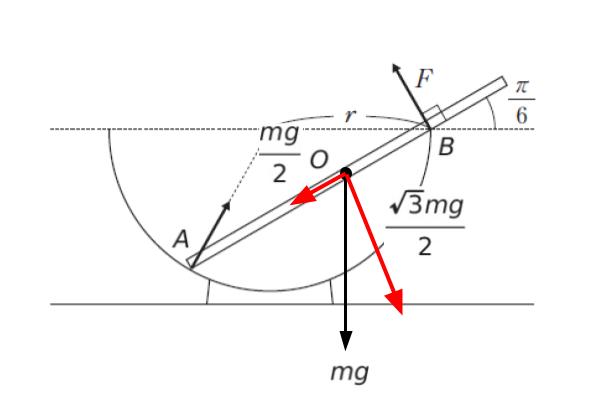
すると、点 A における反力だけ棒に対して斜めなので、この力も縦と横に分解します。点 A における力を FA とおくと、縦の力は FA/2、横の力は √3FA/2 です。
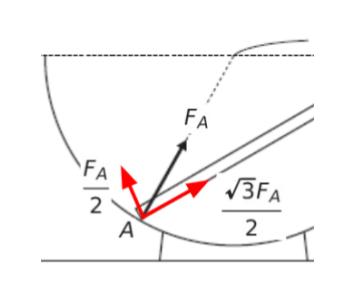
縦の力に注目すると
点 A と点 B における上向きの力の和=点 O における下向きの力 です。
FA/2 + F = √3mg/2…(1)
横の力に注目すると
点 A における右向きの力 = 点 O における左向きの力 です。
√3 FA/2 = mg/2…(2)
(1),(2) より
F = √3mg/3 です。計算過程の一例は以下の通りです。

以上より、正解は 2 です。

コメント