問 題
実数 x,y が (x – 1)2 + (y- 2) 2 ≦ 1 を満たすとき、x2 + y2 の最大値はいくらか。
1. 4 + 2√2
2. 10
3. 6 + 3√2
4. 6 + 2√5
5. 4 + 3√5
正解 (4)
解 説
・(x – a)2 + (y – b)2 = r2 は
『中心 (a,b)、半径 r の円』を表します。
・不等式は、ある点が不等式を満たすかどうかで平面を分割した「領域」を表します。
『(x – a)2 + (y – b)2 ≦ r2 は、中心 (a,b)、半径 r の円の内部領域 (境界含む)』を表します。
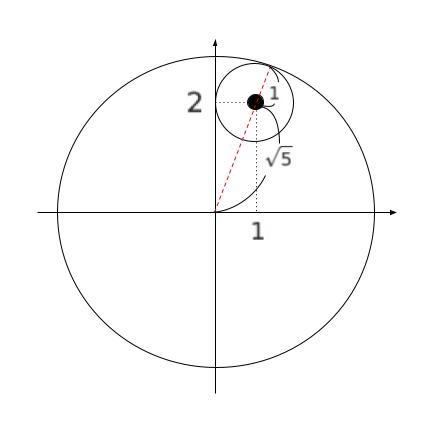
本問は『点 (1,2) を中心として半径 1 の円が置いてある。原点中心の円を少しずつ大きくした時に、先に置いた円に少しでも触れるような条件下で、半径を最も大きくしてください。その時の半径の 2 乗を答えてください。』という問題です。
原点中心の円の半径が最大になるのは「外接」する時です。以下の図から半径は (√5 + 1) です。 2 乗すると「(√5 + 1)2」です。
(√5 + 1)2
= 5 + 1 + 2√5
= 6 + 2√5
以上より、正解は 4 です。

コメント