問 題
△ ABC において、AB = 4、AC = 3、BC = 5 とする。∠BAC の二等分線と辺 BC との交点を D とするとき、線分 AD の長さはいくらか。
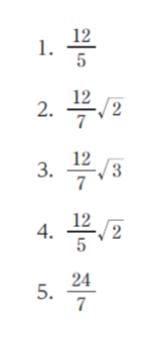
正解 (2)
解 説
辺の長さの比が 3:4:5 なので、∠A = 90° の直角三角形です。
△ ABC の面積は 3 × 4 ÷ 2 = 6 です。
角の二等分線についての基礎知識
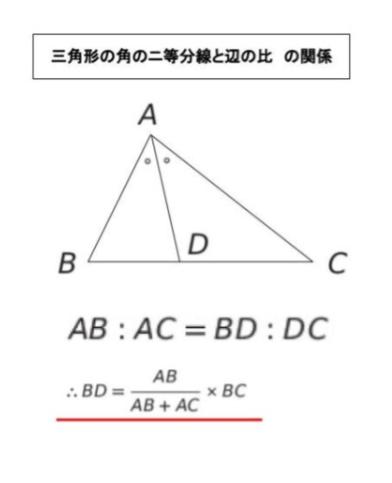
∠BAC の二等分線と BC の交点を D とする時
BD = 4/(4+3) × 5 = 20/7
CD = 5 – 20/7 = 15/7 です。
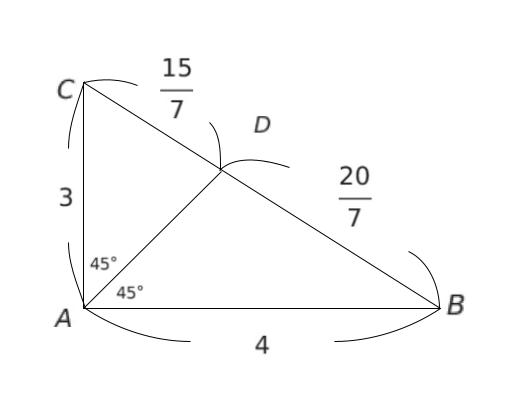
問われているのは AD なので、AD = x とおきます。∠A =90° なので、∠BAD = ∠CAD = 45° です。点 D から AB、AC に向かい垂線を引くと、以下のようになります。
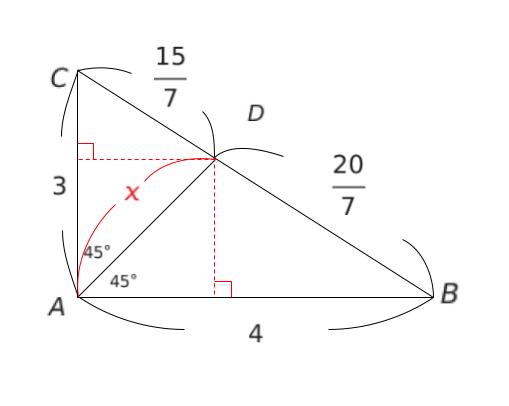
x を斜辺とする直角二等辺三角形 が 2 つできています。
下ろした垂線の長さは x/√2 です。
△ACD の面積は 3 × (x/√2) ÷ 2…(1) です。
△ABD の面積は 4 × (x/√2) ÷ 2…(2) です。
(1) + (2) が△ ABC の面積なので
(1) + (2) = 6 です。
従って
x = 12√2/7 です。
以上より、正解は 2 です。

コメント