2023年 国家一般職(高卒 技術) No.11 物理　解説

　問 題　　　　　

水平な床の上で、小球を水平面となす角 30° で発射したところ、小球は t 秒後に発射地点から 8.5 m先で初めて床に衝突した。このとき、t として最も妥当なのはどれか。ただし、重力加速度の大きさを 10 m/s² 、√3 = 1.7 とする。

1． 0.50
2． 1.0
3． 1.4
4． 1.7
5． 2.7

 

 

 

 

 

　解 説　　　　　

斜めに玉を投げるのは「斜方投射」です。斜方投射では、垂直方向と水平方向に分けて考えるのが基礎知識です。初速 を v₀ とおき、垂直方向と水平方向に分けるとそれぞれ v₀/2、√3v₀/2 と表すことができます。

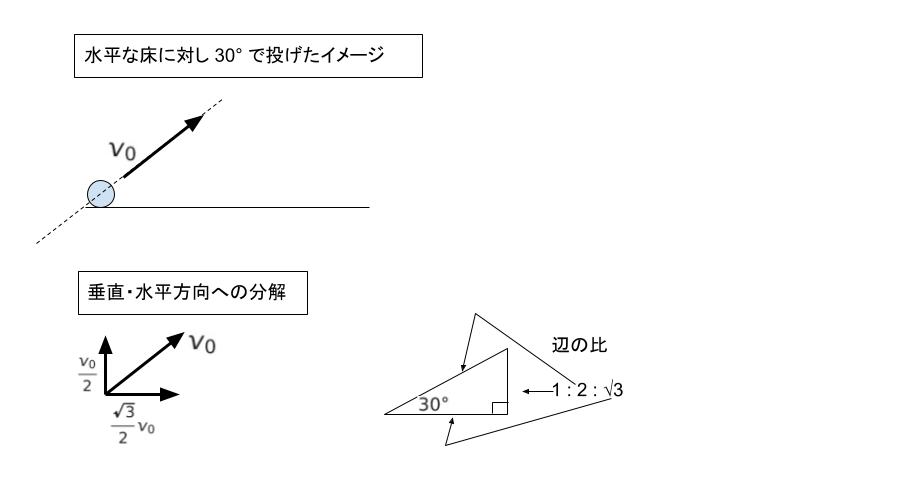
垂直方向に注目します。
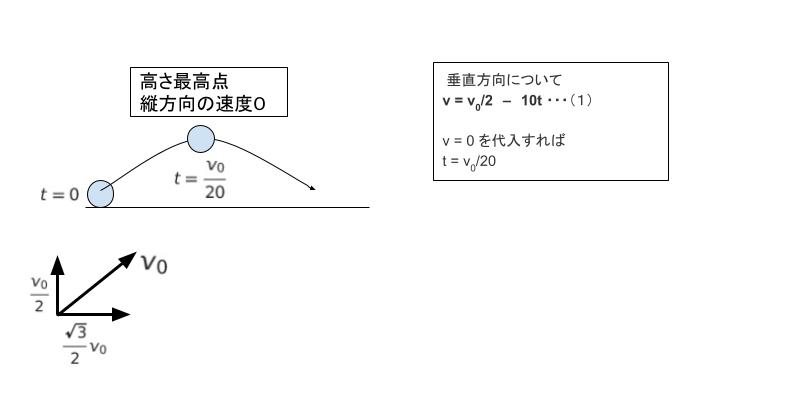
垂直方向について、加速度は重力加速度 10 です。初速 v₀/2、加速度 10 であれば、時刻 T における速さは v = v₀/2– 10T ・・・（１）です。※ 通常小文字の t が時刻ですが、問題文で既に t に意味があるので大文字 T としています。

↗️↘️ と玉は飛んでいくのですが、高さ最高点において、垂直方向の速度は 0 です。（１）において v = 0 として T を求めれば T = v₀/20 です。

「↗️：高さ０ → 最高点」までかかった時間が v₀/20 なので、「↘️：最高点 → 高さ０」までにかかる時間もやはり v₀/20 です。つまり、初めて床に到達するまでにかかった時間は v₀/20 + v₀/20 = v₀/10 と表すことができます。

水平方向は、等速直線運動です。
つまり、√3 = 1.7 とすれば 初速 (1.7/2) × v₀ でずっと進んでいきます。水平方向に進んだ距離は「速さ × 時間」で表されます。

初めて地面につくまでかかった時間は v₀/10 秒です。1.7/2 は 0.85 です。速さを以下 0.85 v₀ と表します。すると水平方向に進んだ距離「0.85 v₀ × v₀/10」＝ 0.085 v₀² ・・・（２）です。問題文より （２）は 8.5 m だったので、（２）＝ 8.5 を解けば、v₀² = 100 → v₀ = 10 とわかります。（妄想なんですが、30° 方向にボール投げたり打ったりして 8.5m 先まで飛んだ時に「物理の理論上、初速 10m/s だったね」とか実際のグラウンドで言われたら、びっくりですよね！）

求める時間は t = v₀/10 なので、10/10 = 1 とわかります。

以上より、正解は 2 です。