問 題
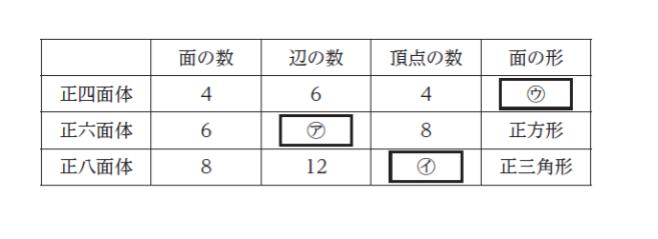
表は、正四面体、正六面体、正八面体のそれぞれの面の数、辺の数、頂点の数、面の形を示したものである。表中の ㋐、㋑、㋒ に当てはまるものの組合せとして正しいのはどれか。
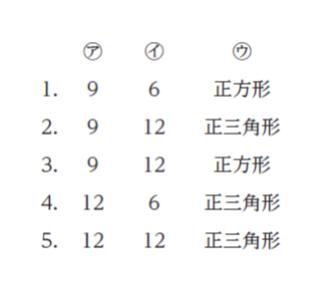
正解 (4)
解 説
参考【正多面体の基礎知識】
・正多面体:正四面体、正六面体、正八面体、正十二面体、正二十面体 の5種類
・面の数は、◯面体 の ◯ と等しい。
・辺の数は 「(一面の辺の数 × 面の数) ÷ 2」
正十二面体の辺:1面は五角形なので 5 × 12 ÷ 2 = 30
正二十面体の辺:1面は三角形なので 3 × 20 ÷ 2 = 30
・頂点の数は 「(辺の数ー面の数) +2」
正八面体の頂点:12 ー 8 + 2 = 6
ーーー
㋐ ですが
正六面体の辺の数が問われています。立方体の見取り図を書いて数えると 12 本 です。正解は 4 or 5 です。また、これにより、㋒ が 正三角形とわかります。
㋑ ですが
正八面体の頂点の数が問われています。正八面体の見取り図を書いて数えると6個です。

以上より、正解は 4 です。

コメント