2023年 国家一般職(高卒 技術) No.2 数学　解説

　問 題　　　　　

直線 y= √3x + k が円 x² + y² = 1 と共有点をもたないための定数 k の値の範囲として正しいのはどれか。

 

 

 

 

 

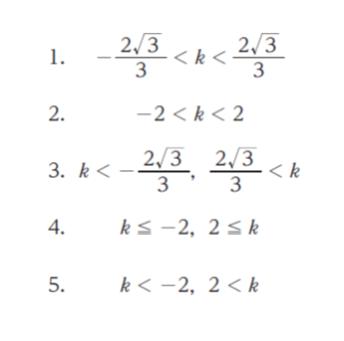
　解 説　　　　　

√3 が 「2 乗したら３になるような数」 → 1.73 ぐらいの数です。大体 y = 1.73x + k で表せる右上がり直線と、中心が (0,0) 半径 1 の円が 交わらないような k の範囲が問われています。

【解法１：連立して判別式を用いる】
共有点を求めるために、２つの式を連立させます。解くために y = √3 x + k を円の方程式に代入し、整理すると 4x² + 2√3 k x + k² -1 = 0 です。解を持つかは判別式です。判別式を D とおけば、D = (2√3k)² ー 4 × 4(k² ー 1) = -4k² + 16 となります。

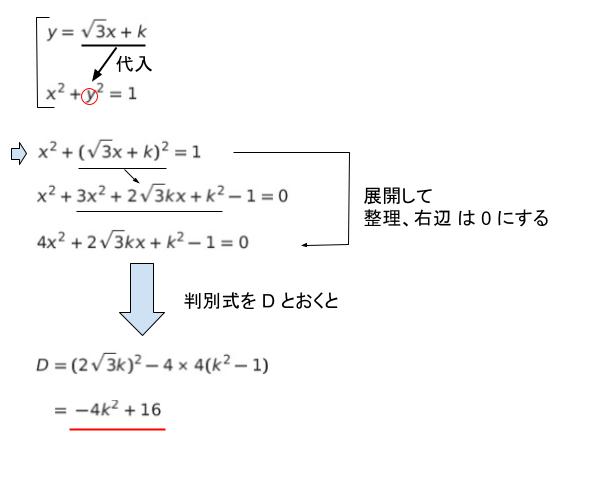
解を持たないとは D < 0 なので、k < -2、k > 2 とわかります。

以上より、正解は 5 です。 

【解法２：選択肢の活用、グラフから推測】
以下のような絵を手元に書くと　k がすごく大きかったり小さかったりすれば、交わらないことはすぐわかるのではないでしょうか。※ y = 1.73x + k は「x = 0 の時に y = k」です。絵における y 軸との交点が k ということです。

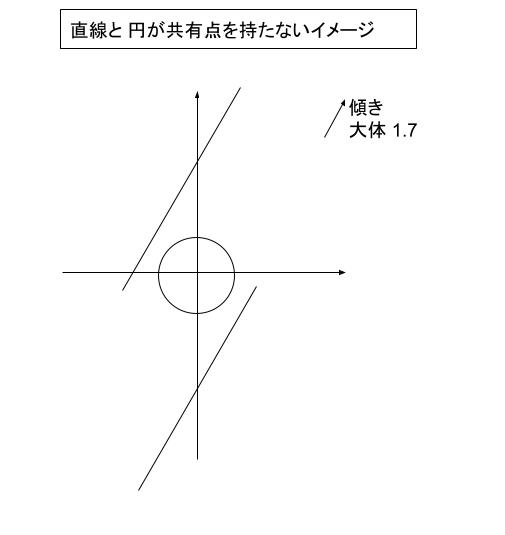
このイメージから、 k がある範囲内となっている、選択肢 1,3 は誤りです。ぜひまずこの２つは誤りと選べるようになりましょう！

ここまででも十分ですが、選択肢を見ると k = 2 の時に共有点を持つかどうかがわかると、さらに選択肢をしぼれます。k = 2 としてみましょう。

できるだけ正確に図を書くと丁度接しそうだとわかるのではないでしょうか。下図のように接します。補足知識で、覚える必要ないのですが、y = √3x の傾きは、x 軸となす角がちょうど 60° です。

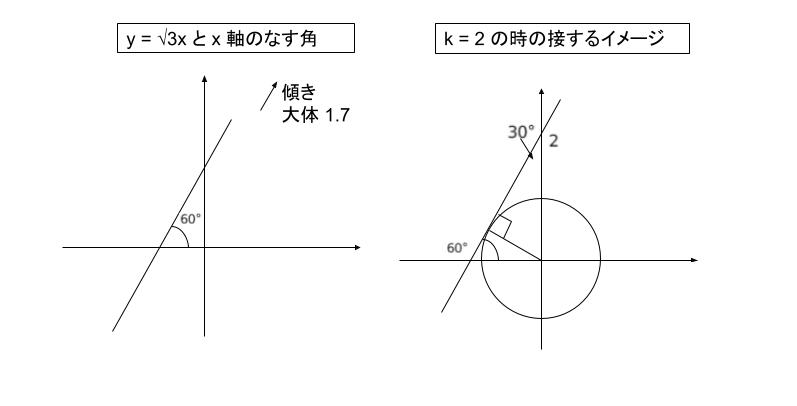
以上より、正解は 5 です。