過去問 2023年 国家一般職（高卒 基礎）No.18解説

　問 題　　　　　

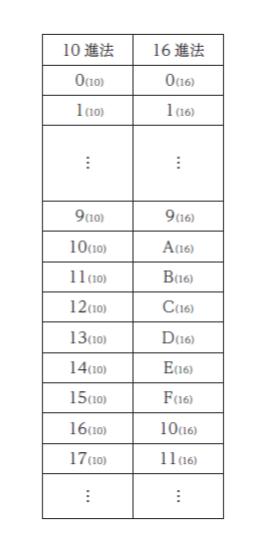
 ａ進法で表された数 Ｘ を、X_（a）と表記するとき、F_（16）を 3_（10）で割ったときの商は 5_（16）と表せる。1C_（16）を 2_（10）で割ったときの商を 16 進法で表したものはどれか。なお、10 進法と16 進法の対応の関係は、次のとおりである。

1．A_（16）
2．B_（16）
3．C_（16）
4．D_（16）
5．E_（16）

 

 

 

 

 

　解 説　　　　　

【n 進数の基礎知識】
n 進数の１桁目は n⁰ が何個あるかを示します。 以下、2 桁目は n¹ が何個あるか・・・です。ちなみに、小数点以下の場合、小数点第一位は n^-1 が何個あるかを示します。以下、小数点第二位は n^-2 が何個あるか・・・を示します。

―――

1C_（16）とは「16⁰ が C 個（つまり 12 個）、16¹ が 1 個ある」ということです。従って、1 × 12 + 16 × 1 = 28 を意味します。

1C_（16）を 2_（10）で割ったときの商を考えます。28 を 2 で割れば 14 です。表より 14 は「16 進数の E」に対応します。

以上より、正解は 5 です。

類題 2022 no18 2 進数、16 進数
https://yaku-tik.com/koumuin/2022-gijyutu-18/