問 題
図Ⅰのように長さ6.0mの単純梁に10kN/mの等分布荷重が作用している。
単純梁の断面は図Ⅱのような幅30cm、高さ50cmの一様な長方形断面である。
このとき、単純梁の断面の下縁に生じる引張応力度が最大となる位置と引張応力度の最大値の組合せとして最も妥当なのはどれか。
ただし、梁の自重は無視できるものとする。
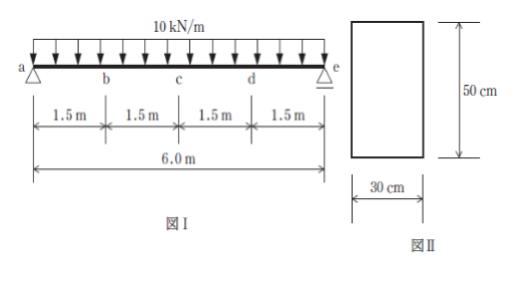
引張応力度が最大となる位置 引張応力度の最大値
1. 点b及び点d 3.6N/mm2
2. 点b及び点d 7.2N/mm2
3. 点c 1.8N/mm2
4. 点c 3.6N/mm2
5. 点c 7.2N/mm2
解 説
引張応力度が最大というのは、M図を書いて最大値をとる所のことです。単純梁、等分布荷重の場合は、M図が以下のような形となることが基本的知識です。
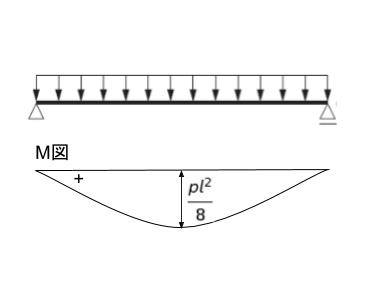
よって、引張応力度が最大となるのは点 c です。
正解は 3~5 です。
引張応力度をσとすると σ = M/Z です。ここで Z は断面係数です。断面係数とは断面二次モーメントを図心から端までの距離で割ったものです。
長方形断面であれば
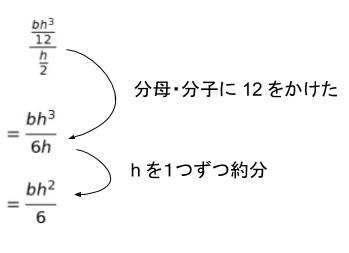
となるので、bh2/6 です。覚えていてもよい式です。
σの計算ですが、選択肢を見ると単位が N/mm2 であることに注意し、単位を N や mm に直して計算していきます。
M = pl2/8 ですが、まず k は 103 なので pを 10000N/m とします。1m = 100cm = 1000mm なので p は 10000N/1000mm =10N/mm です。
また、l が 6m なので6m = 6000mm です。
よって、l2 は 36000000mm2 です。
同様に Z = bh2/6 ですが
b = 30cm = 300mm
h = 50cm = 500mm
h2 = 250000mm 2 です。
準備ができたので代入します。

以上より、正解は 4 です。

コメント