問 題
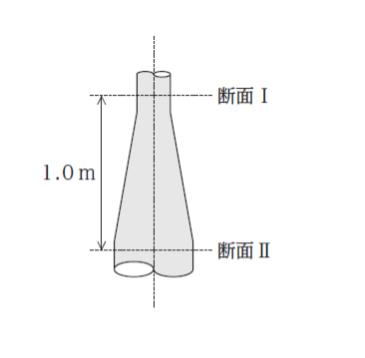
図のように、管の中心軸が鉛直になるように置かれた断面が滑らかに拡大する管内を水が定常流状態で流れている。流量が 50.0 m3/s、断面Ⅰの断面積が 5.0 m2、断面Ⅱの断面積が 25.0 m2 であるとき、断面Ⅰと断面Ⅱの圧力差として最も妥当なのはどれか。
ただし、重力加速度の大きさを 10 m/s2、水の密度を 1.0 × 103 kg/m3 とする。また、損失水頭は無視できるものとする。
1.2.9 kN/m2
2.5.8 kN/m2
3.29 kN/m2
4.58 kN/m2
5.290 kN/m2
正解 (4)
解 説
流体で圧力が関わっていることからベルヌーイの定理を思い出します。ベルヌーイの定理より v12/2g + z1 + p1/ρg = v22/2g + z2 + p2/ρg です。これは基礎知識です。また、連続の式 Q=AV です。
断面 Ⅰ と中心軸が交わる点を A、断面 Ⅱ と中心軸が交わる点を B とし、A 及び B において、まず連続の式より v がそれぞれの点において vA = 10 m/s、vB = 2 m/s とわかります。
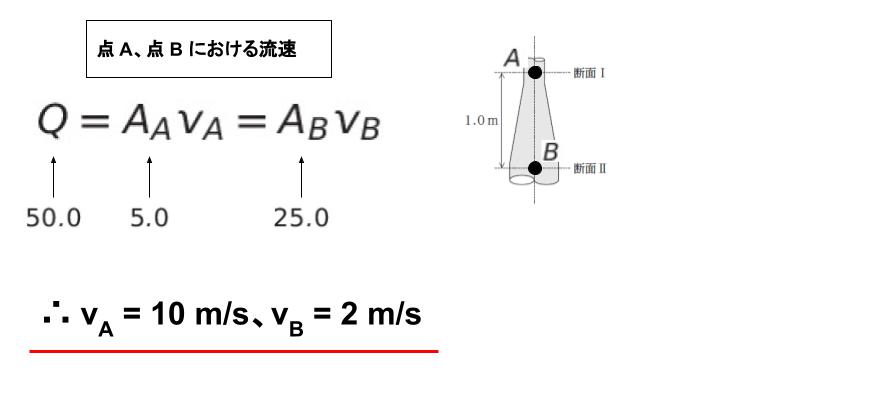
これをふまえベルヌーイの定理を考えれば、圧力差 PB ー PA = 58k とわかります。点 B を位置の基準とおくため、ZB = 0 です。問題文の値を代入して計算する流れの大枠は、以下の通りです。

以上より、正解は 4 です。

コメント