問 題
tanθ=3のとき
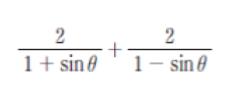
の値はいくらか。
- 30
- 40
- 50
- 60
- 70
正解 (2)
解 説
式は分母が違う足し算、つまり 2/3 + 2/5 みたいなものなので、まずは通分してみます。
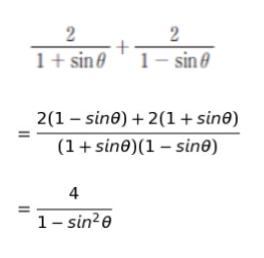
解法1【1-sin2θ に注目する】
「sin2θ+cos2θ = 1」 より 1-sin2θ = cos2θです。tanθとcosθの関係といえば、1+tan2θ = 1/cos2θ です。
tanθ = 3 なので、1+32 = 1/cos2θです。
よって
10 = 1/cos2θ・・・(1) です。
求めるのは 4/cos2θなので(1)の両辺を4倍すれば、40となります。
正解は 2 です。
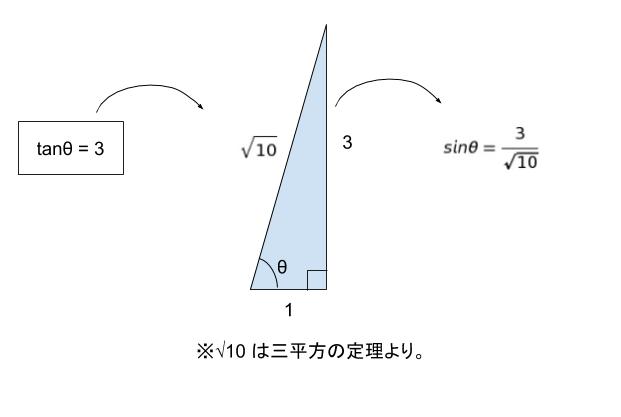
解法2【tanθがわかっているので直角三角形を考える】
tanθ = 3をみたす直角三角形とは、直角をなす2辺の比が1:3ということです。すると斜辺の長さは√10とわかります。三辺の長さがきまればsinθを求めることができます。
sinθ = 3/√10 です。
求めたいのは 4/(1-sin2θ) です。sinθ = 3/√10 なので、sin2θ = 9/10 です。1-sin2θ = 1/10 となります。
従って、
4/(1-sin2θ)
=4/(1/10)
=40 です。
正解は 2 です。

コメント