問 題
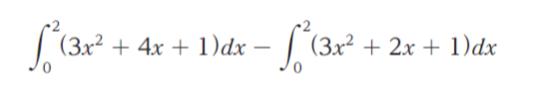
はいくらか。
1.2
2.4
3.6
4.8
5.10
正解 (2)
解 説
まず、小さな数字が ∫ の横についてない形の 「∫ 式 dx」 を計算します。不定積分の計算といいます。不定積分は「微分したら式になるのはなんだ?」という計算と考えればよいです。∫ xn dx = xn+1/(n+1) が基本公式です(参考 2021 no7)。

不定積分が終わったら、小さな数値を処理します。そこまでやるのが「定積分」です。小さな数値の処理ですが、不定積分の結果 に対して「上の数値を代入した値」ー「下の数値を代入した値」と計算すれば OK です。
上の数値 x = 2 を代入すると、それぞれ 18、14 です。下の数値 x = 0 を代入すると 共に0です。「上の数値を代入した値ー下の数値を代入した値」はそれぞれ 18,14 となります。従って、求める値は 18 – 14 = 4 となります。
以上より、正解は 2 です。
ーーーーーーーーーーーー
※ 小さな数字の部分が各項ともに0と2なので、中身を先に引き算しても、積分のルール上 OK です。
まず「3x2 + 4x + 1」ー「3x2 + 2x + 1」を計算します。すると 2x です。∫20 2x dx を計算すればよいということです。
不定積分すると x2 になります。定積分の数値計算のため、x = 2 を代入すると 4、x = 0 を代入すると 0 なので、4-0=4 が答えです。
以上より、正解は 2 です。

コメント