問 題
電磁誘導に関する次の記述の ㋐、㋑、㋒ に当てはまるものの組合せとして最も妥当なのはどれか。
「電磁誘導によってコイルに生じる誘導起電力の大きさは、コイルの巻数に ㋐ し、コイルを貫く磁束の時間に対する変化の割合に ㋑ する。これを電磁誘導に関するファラデーの法則という。
巻数が 200 回のコイルを貫く磁束を 5 秒間に 1.0 Wb の一定の割合で変化させたとき、コイルに 40 V の誘導起電力が生じた。このコイルを貫く磁束を 4 秒間に 1.0 Wb の一定の割合で変化させたとき、コイルに生じる誘導起電力は ㋒ である。」
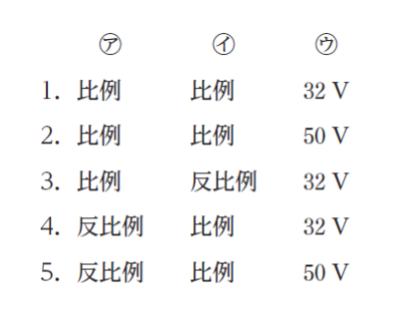
正解 (2)
解 説
巻数 N のコイルにおいて生じる誘導起電力は V = N(dΦ/dt)です。dΦ/dt は、時間当たりの磁束の変化割合です(ファラデーの法則)。つまり、V は N 及び dΦ/dt に比例します。これは基礎知識です。従って、㋐、㋑ 共に比例です。正解は 1 or 2 です。
5 秒間に 1.0 Wb の変化=0.2 Wb/秒 が 4 秒間に 1.0 Wb の変化 = 0.25 Wb/秒 になっています。つまり、時間当たり磁束変化割合 dΦ/dt が「0.25 ÷ 0.2 = 1.25 倍」になっています。従って、誘導起電力も比例して増えて 1.25 倍になります。40 × 1.25 = 50 です。
以上より、正解は 2 です。

コメント