問 題
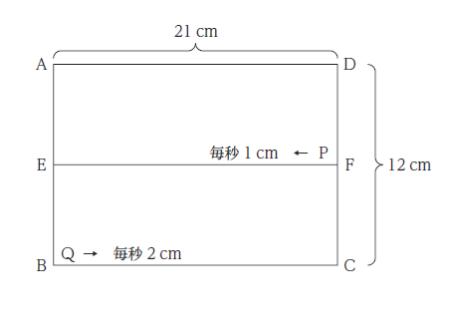
図のような縦 12 cm、横 21 cm の長方形 ABCD があり、辺 AB の中点をEとし、辺 CD の中点をFとする。点Pは線分 FE 上を点Fの位置から毎秒 1 cm の速度で、点Qは辺 BC 上を点Bの位置から毎秒 2 cm の速度で同時に移動する。このとき、三角形 APQ の面積が、最初に長方形 ABCD の面積の 7 分の 1 になるのは、点P及び点Qが移動を始めてから何秒後か。
1. 6 秒後
2. 6.5 秒後
3. 7 秒後
4. 7.5 秒後
5. 8 秒後
解 説
動く点について、方程式を立てて考えるのは面倒なので、選択肢の活用がおすすめです。
まず、動く点について考えなくても分かる部分を求めます。長方形 ABCD の面積の 7分の1は、12×21÷7=36です。
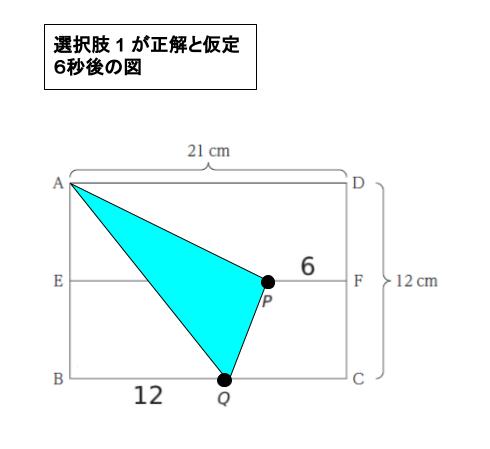
選択肢 1 が正解と仮定します。
6秒後は、以下のような位置関係です。これを見て、△ APQ の面積を求めます。
点 P から AB と平行に縦補助線を引き、AD との交点を R、BC との交点を S とします。外側の長方形 ABSR(面積 12 × 15 = 180)から △ABQ、△ARP、△PQS の面積を計算して引きます。以下の図を参考に、各自ぜひ計算してみてください。四角で囲まれた数字が、各部分の面積です。
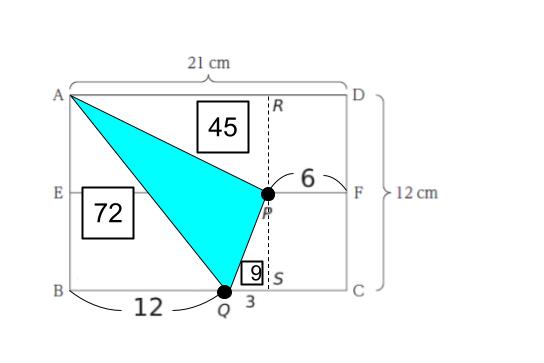
すると、6秒後 △ APQ の面積は54です。選択肢 1 は誤りです。
同様に各選択肢を検討すればよいのですが、整数秒 後 の方が計算は簡単なので、次は選択肢 3 の「7秒後」に注目するのがおすすめです。7秒後は丁度 PQ がまっすぐ並ぶこともあり、△APQ の面積はすぐ計算できて 42 です。選択肢 3 は誤りです。
後は選択肢 5 が正解と仮定し、8秒後を考えて計算すれば、面積30となります。(P が Q の左側になるので、点 Q から AB と平行に補助線を引いて計算します)。ぜひ各自計算にトライしてみてください。
ここまでの結果をまとめると
・6秒後→54
・7秒後→42
・8秒後→30 となります。
選択肢の範囲では、時間が経過するほど △APQ の面積が減少していくという傾向が読み取れます。従って、△ APQ の面積が 36 となるのは、7秒後から8秒後の間です。つまり、正解は 7.5 秒後と考えられます。
以上より、正解は 4 です。

コメント