問 題
1 ~ 7 の互いに異なる数字が一つずつ書かれた 7 枚のカードがある。これらのカードのうち、 6 枚をA、Bの 2 人に 3 枚ずつ配ったところ、Aに 6 のカードが配られ、AとBに配られたカードの数字の和は等しかった。さらに、AとBがカードを 1 枚交換したところ、Aが持っているカードの数字の和は、Bが持っているカードの数字の和の 3 倍となった。このとき、配られなかったカード 1 枚と、交換したカード 2 枚の、合計 3 枚のカードに書かれた数字の和はいくらか。
1. 9
2. 10
3. 11
4. 12
5. 13
解 説
具体的に考え、カード交換後の条件がとても厳しいとわかるかどうかで解く時間が大きく左右される問題と思われます。
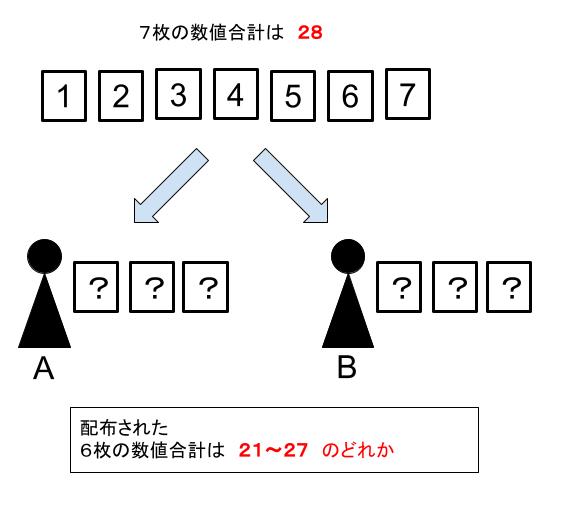
7枚のカードの合計は、1+2+3+4+5+6+7=28です。7枚のうち1枚を除き A,B に3枚ずつカードが配られるので、A と B のカードの数値を合計すれば、最小21(配られなかったカードが7の場合)、最大27(配られなかったカードが1の場合)です。(参考図1)。
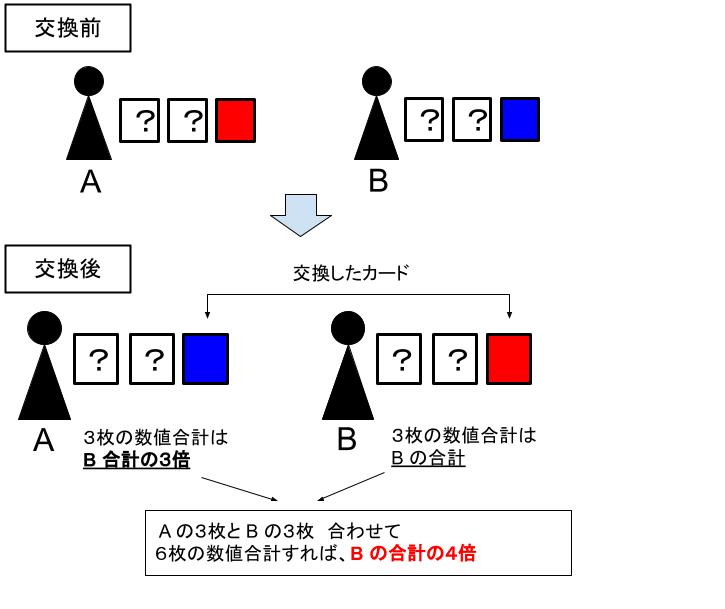
A,B が1枚ずつカード交換を行った後に「A のカード合計が、B のカード合計の3倍」となります。そのため、A,B の全ての数字を足せば、B のカード合計の4倍です。言い換えれば4の倍数です。
21~27の中で4の倍数は24のみです。つまり、カード交換後、B のカードの合計は6です。A のカードの合計は18です。配られなかったカードは4です。
カード合計6となる組み合わせは「1,2,3」です。同様にカード合計18となる組み合わせは「5,6,7」です。
交換後が分かったので、交換前を考えれば、交換したカードは1と7です。交換前は A「1,5,6(合計12)」、B 「2,3,7(合計12)」だったとわかります。
求めたい「配られなかったカード 1 枚と、交換したカード 2 枚の和」は「4+(1+7)」なので、12です。
以上より、正解は 4 です。

コメント