問 題
消費者Aと消費者Bの二人の消費者,そしてX財とY財の二つの財から成る経済を考える。消費者AによるX財の消費量を xA,Y財の消費量を yA,消費者BによるX財の消費量を xB,Y財の消費量を yB とすると,消費者A,Bの効用関数は,それぞれ
uA = 4xAyA,uB = 9xByB
である。ただし,xA > 0,xB > 0,yA > 0,yB > 0 とする。また,X財の総量が 16,Y財の総量
が 9 であり,それらを二人で配分するものとする。
この経済の効用フロンティア(パレート最適な状態における二人の消費者の効用水準の組合せ)を
表す式として妥当なのはどれか。
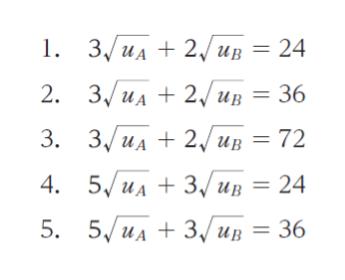
解 説
パレート最適とは、2者の場合であれば、1人の効用を上げようとすると、もう1人の効用が下がるような状態のことです。
『効用フロンティアの式の求め方』という知識を準備してきた人は少ないと思われます。試験本番において有効的である考え方として「選択肢を活かし、正解らしき式を見つける」という戦術で、以下解説します。
選択肢から、uA と uB に関する式とわかるので、具体的、かつ、簡単な値として uA = 0 の場合を考えてみます。この時、xA,yA のどちらかが 0、もしくは両方が 0 です。(xA > 0,yA > 0 という条件があるので、気になる人は「限りなく 0 に近づけた値」と 0 を読み替えて考えればよいです。)。
xA,yA のうち一方が 0 で、他方が 0 以外の定数である場合を考えます。すると、定数分を B に配分すれば、より B の効用があがる一方で、A の効用は 0 のままかわりません。このような状況においては、1人の効用が下がらずに、もう1人の効用を上げることができるため、パレート最適ではありません。従って、xA,yA の 両方が 0 で、X 財、Y 財全てを B に配分して、B の効用を最大化した場合がパレート最適です。
今考えたパレート最適の場合、具体的な各値は、xA = yA = 0、xB = 16、yB = 9 の時、uA = 0 、uB = 9 × 16 × 9、√uB = 9 × 4 = 36 です。選択肢に uA = 0、√uB = 36 を代入した時、右辺と等しくなるのは、3 √UA + 2 √UB = 72 です。
以上より、正解は 3 です。

コメント