問 題
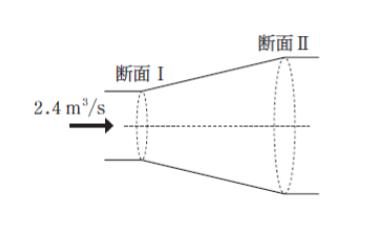
図のように、管の中心軸が水平になるように置かれた断面積が滑らかに拡大する管内を水が定常状態で流れている。
流量が 2.4 m3/s、断面Ⅰの断面積が 0.30 m2、断面Ⅱの断面積が 1.20 m2、断面 Ⅰ における圧力が 100 kN/m2 であるとき、断面Ⅱにおける圧力はおよそいくらか。
ただし、水の密度を1.0 × 103 kg/m3 とし、エネルギー損失は無視できるものとする。
1. 30 kN/m2
2. 70 kN/m2
3. 100 kN/m2
4. 130 kN/m2
5. 170 kN/m2
正解 (4)
解 説
ベルヌーイの定理より
v12/2g + z1 + p1/ρg = v22/2g + z2 + p2/ρg です。これは基礎知識です。
本問では z1 = z2 なので
v12/2g + p1/ρg = v22/2g + p2/ρg と簡略化できます。さらに両辺に g をかけておけば
v12/2 + p1/ρ = v22/2 + p2/ρ です。
また、連続の式 Q=AV です。
流量が 2.4 で、断面Ⅰに注目すれば 断面積が 0.30 なので v = 8 m/s です
断面Ⅰと断面Ⅱの面積の比は1:4なので、速度の比が4:1とわかります。
断面Ⅰの流速が 8 m/s なので、断面Ⅱの流速は 2 m/s です。
以上より、p2 以外の変数の値が全てわかったので、代入して計算します。

以上より、正解は 4 です。

コメント