H30年 国家一般職(高卒 技術) No.1 数学　解説

　問 題　　　　　

2 次方程式 3x²– 8x – 16 = 0 の二つの解が α、β であるとき

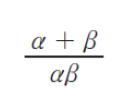
はいくらか。

 

 

 

 

 

　解 説　　　　　

与えられた 2 次方程式は
(3x＋４)(x ー 4) = 0 と因数分解できます。従って、x = ー4/3、4 が解です。

小さい方から α、β とおき、α = -4/3、β = 4 とします。
α + β = 8/3 です。αβ は -16/3 です。
従って （α + β）/αβ　は -1/2 です。

今回は運良く因数分解できたのですが
うまく方程式が解けないこともあります。
その場合は、解と係数の関係を用いて解きます。

「ax² + bx + c = 0 の解を α、β とおくと
α + β = -b/a、αβ = c/a」 です。
これを解と係数の関係と呼びます。この機会にぜひおさえておきましょう！

a = 3、b = -8 より、α + β = 8/3 です。
a = 3、c = -16 より、αβ は -16/3 です。
従って （α + β）/αβ　は -1/2 となります。

実際の解である 「x = ー4/3、4」を求めずに答えが出ている点に注目してください。

以上より、正解は 3 です。