問 題
高校生の A と B の 2 人は、通学の際、K駅から同じ道を 1,800 m 進んで高校に向かう。ある日の状況が次のとおりであったとき、B の走る速さと A の歩く速さの差はいくらか。ただし、2 人の時計は正確な時刻からずれているものの、そのずれはそれぞれ一定であるものとする。
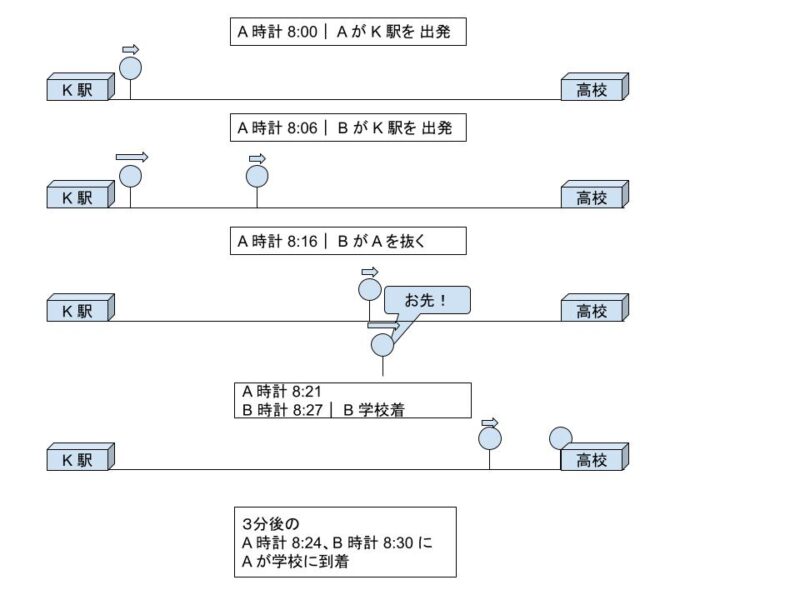
○ A は、K 駅を A の時計で 8:00 に出発し、一定の速さで歩いて高校に向かったが、A の時計で 8:16 に B に追い抜かれた。
○ B は、A が K 駅を出発するのを見届けてから 6 分後に同駅を出発し、一定の速さで走って高校に向かった。途中で A を追い抜き、その 5 分後に高校に到着した。A の到着はB の到着より 3 分遅く、Bの時計で 8:30 であった。
1.分速 36 m
2.分速 39 m
3.分速 42 m
4.分速 45 m
5.分速 48 m
解 説
問題文を読んで図示して状況整理すると、時計がずれていることはあまり関係なく「A は 1800 m を 24 分かけて移動」「B は 1800 m を 15 分かけて移動」したことが読み取れれば、答えを出せる問題です。一例として、以下のようにまとめることができます。
後は A,B の分速を出して、差を求めてもよいのですが、以下の解き方が 片方の分速だけで求めることができて少し計算が楽になります。ぜひ参考にしてみてください。
かかった時間の逆比が速さの比となります。これは基礎知識です。かかった時間の比が24:15=8:5です。そのため、A の速さ:B の速さは5:8です。速さの差は、比で言う3となります。
B の速さを求めると、1800 m を 15 分なので 1800 ÷ 15 = 120 m/分 です。比で言う 8 が 120 m/分 なので、比で言う1は 15 m/分 です。求めたい「速度の差」は「比で言う3」だったので、15 × 3 = 45 です。
以上より、正解は 4 です。

コメント