問 題
A、B、C の 3 人が 1 ~ 6 の目を持つサイコロをそれぞれ 2 回振り、出した二つの目の積をそれぞれの得点とした。それぞれの出した二つの目と得点について、次のことが分かっているとき、確実にいえるのはどれか。
○ A、B、C について、それぞれが 1 回目に出した目は 2 回目に出した目よりも小さかった。
○ Cは、1 回目に A の 1 回目と同じ目を出し、2 回目に B の 2 回目と同じ目を出した。
○ A、B、C について、得点は 4 の倍数であった。
○ A の得点は、Bと同じであったが、C とは異なっていた。
1.A は、1 回目に 4 の目を出した。
2.A と C の得点の差は、8 点であった。
3.B は、2 回目に 6 の目を出した。
4.B と C が 1 回目に出した目の差は、2 であった。
5.C は、2 回目に 4 の目を出した。
解 説
箇条書きの条件を上から、条件1、条件2・・・、条件4とします。
・条件1より、1回目に6、2回目に1は出ていません。
・A の1回目が1だったとします。
条件3 の「4の倍数」を満たすため、 A の2回目は4しかありません。C の1回目も条件2より1で、4の倍数を満たすために C の2回目も4しかありません。すると条件4より A と C の点数は同じではない という条件に矛盾します。従って、A の1回目は1ではありません。同様に、A の1回目は3や5でも、うまくいきません。やや絞れてきました!
・A の1回目が2と仮定します。
4の倍数を満たすため、A の2回目は4 or 6 です。条件4の 積について A = B を満たすように A の2回目を6、B を3,4とします。すると C の1回目は2なので、4 の倍数を満たすため、C 2 回目は4で条件を満たします。1つ組み合わせを見つけました!
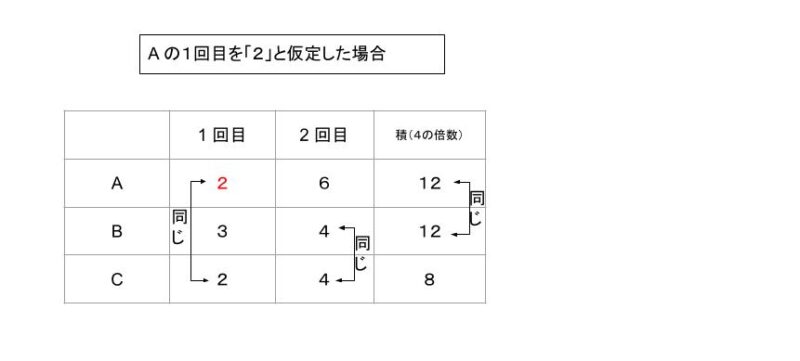
以下、選択肢 を検討します。
選択肢 1 ですが
A 1 回目は2です。選択肢 1 は誤りです。
選択肢 2 ですが
A と C の得点差は4点です。選択肢 2 は誤りです。
選択肢 3 ですが
B 2回目は4です。選択肢 3 は誤りです。
選択肢 4 ですが
B,C 1 回目の差は1です。選択肢 4 は誤りです。
選択肢 1 ~ 4 誤りなので
以上より、正解は 5 です。

コメント