問 題
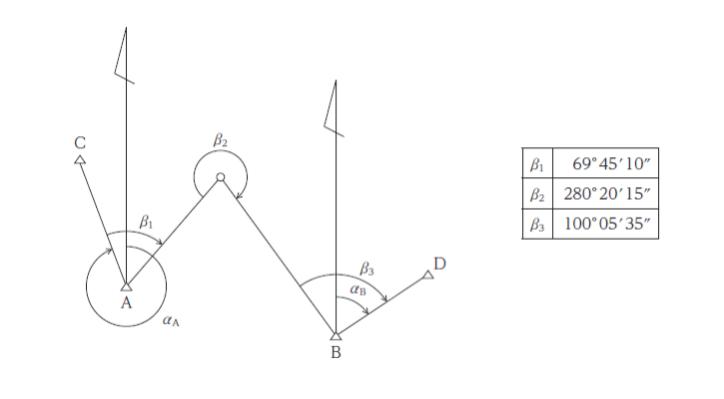
図のように、既知点 A から既知点 B に結合トラバース測量を行ったところ、表の結果を得た。A の既知方位角 αA が 330° 25 ‘ 05 ‘ ‘ であり、B の既知方位角 αB が 60° 35 ‘ 45 ‘ ‘ であるとき、測角の誤差(閉合誤差)として最も妥当なのはどれか。
1.-15 ‘ ‘
2.-5 ‘ ‘
3.+5 ‘ ‘
4.+10 ‘ ‘
5.+20 ‘ ‘
解 説
トラバースは「横切る」などの意味です。山の斜面を登ったり降りたりしつつ横切っていくイメージです。
トラバース測量は、初めの基準点から順に点を測定し、折れ線(トラバース)を作って測定する方法です。各折れ線の長さ、方位角(北を基準とした角度)などを用いて、各点の座標を見つけます。角度は 1° = 60′ 1′ = 60” です。
トラバース測量の問題では、とりあえず折れてる所にはまっすぐ北を向く補助線を書き込みます。本問では β2 の所に線がないので書き込むと以下のようになります。線分 CA と北向きの線のなす角は 360° から αA を引けば 29° 34′ 55” とわかるので書き込んでいます。
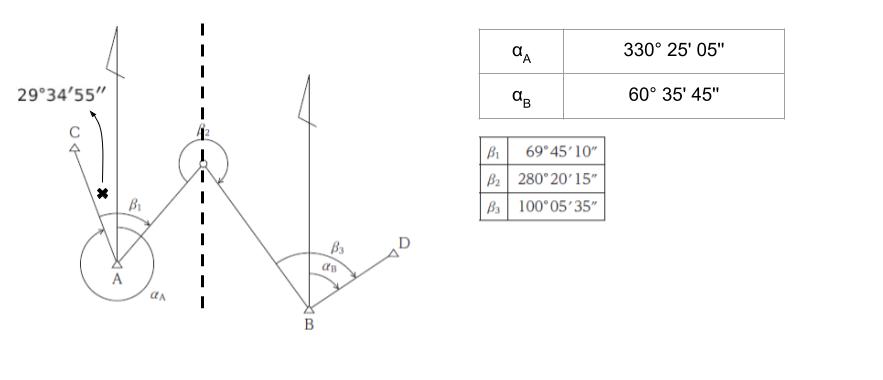
錯角が等しいので β2 の周りに注目すると、以下のようになります。
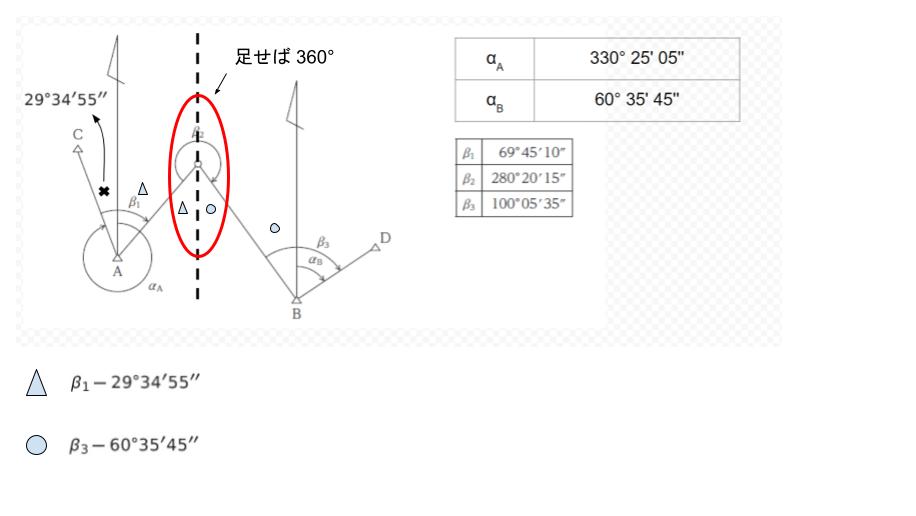
(β1 – 29° 34′ 55”) + β2 + (β3 ー 60° 35′ 45”) = 360 のはず です。ーの所を計算すれば ー 90° 10′ 40” です。
表の β1 ~ β3 値を足すと
69° 45′ 10” + 280° 20′ 15” + 100° 05′ 35”
= 450° 11′ 00” です。
従って
(β1 – 29° 34′ 55”) + β2 + (β3 ー 60° 35′ 45”)
= 450° 11′ 00” ー 90° 10′ 40”
= 20” となります。測角の誤差(閉合誤差)は + 20” です。
以上より、正解は 5 です。

コメント