問 題
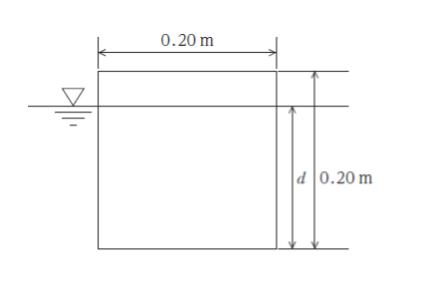
図のように、一辺が 0.20 m の正方形断面をもつ長さ 2.0 m の一様な角材を水に浮かべたとき、きっ水 d として最も妥当なのはどれか。ただし、重力加速度の大きさを 10 m/s2、水の密度を 1.0 × 103 kg/m3、角材の密度を 6.0 × 102 kg/m3 とする。
1. 0.10 m
2. 0.12 m
3. 0.14 m
4. 0.16 m
5. 0.18 m
解 説
【浮力の基礎知識】
液体が出てきたら浮力です。浮力を F浮 と表すと F浮 = ρVg です。この公式における ρ は、押しのけられた液体の密度です。また、V は、押しのけられた液体の体積です。
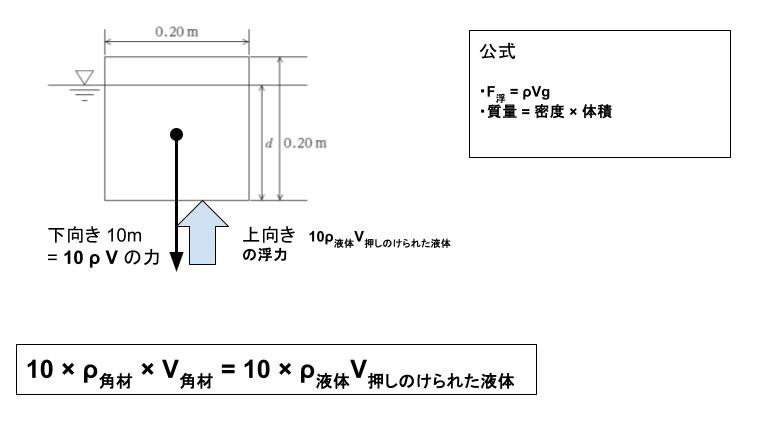
角材は 質量を m とすれば 下向き mg の力が作用します。問題文より g = 10 なので、下向き 10 m の力が作用します。
角材が水に浮かんでいるということは、下向き 10m の力と、上向きの F浮力 = 10 ρ液体 V押しのけられた液体 が等しいということです。ここで、質量とは 密度 × 体積です。これは基礎知識です。そのため、m = ρ角材 V と表します。すると 10 × ρ角材 × V = 10 × ρ液体 V押しのけられた液体 です。
水の密度と角材の密度の比が
1.0 × 103 : 6.0 × 102 → 1000:600 = 5:3です。等式の密度の所に右辺は5,左辺は3が入ると考えると理解しやすいと思います。
すると、等式が成り立つ時 V角材:V押しのけられた液体 は 5:3 です。断面積で考えれば、以下の部分の比が5:3ということです。
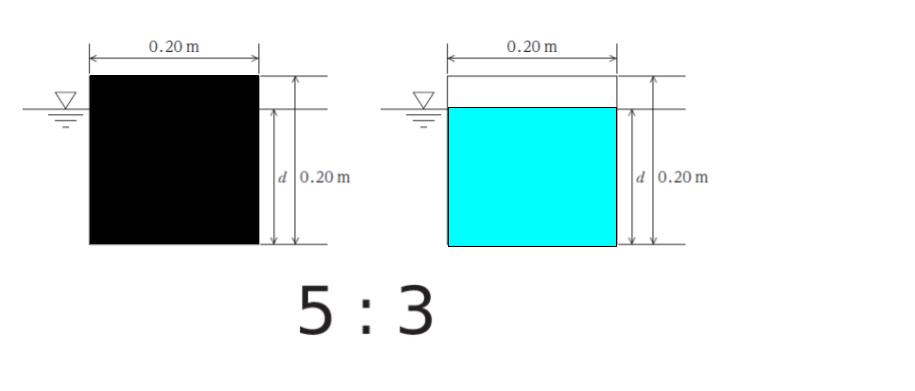
すると高さの比も5:3です。比で言う5が 0.20 m なので、比で言う1が 0.04 m です。そのため、比で言う3は 0.12 m となります。
以上より、正解は 2 です。
類題 2019 no64 浮力
https://yaku-tik.com/koumuin/2019-gijyutu-64/

コメント