2023年 国家一般職(高卒 技術) No.61 土木基礎力学　解説

　問 題　　　　　

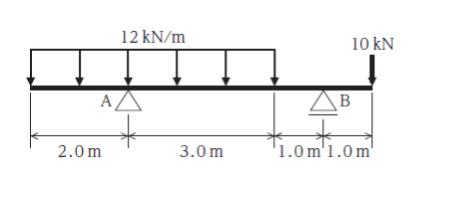
図のように、張出し梁に鉛直集中荷重と等分布荷重が作用しているとき、支点 B の鉛直反力の大きさとして最も妥当なのはどれか。ただし、梁の自重は無視するものとする。

1．20 kN
2．25 kN
3．30 kN
4．35 kN
5．40 kN　

 

 

 

 

 

　解 説　　　　　

まず反力を求めます。支点 A の反力を R_A、支点 B の反力を R_B とします。

反力を求める際は、等分布荷重は集中荷重に直します。12 kN/m が 5.0 m にわたっているので 12 × 5.0 = 60 kN の集中荷重に直します。作用するのはちょうど真ん中です。以下のように直します。

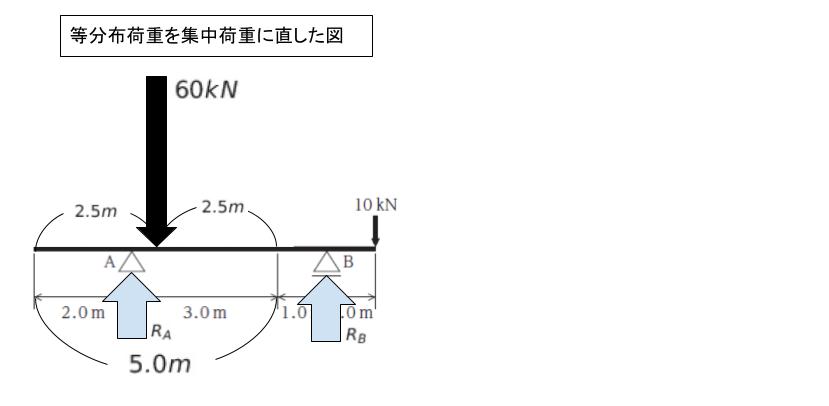
縦方向の力に注目すれば
R_A + R_B = 60 + 10・・・（１） です。

モーメントは「力 × 距離」です。点 A 周りのモーメントに注目すれば、各力によるモーメントはそれぞれ、以下のように計算することができます。

・下向き 60kN の力により 60 × 0.5 = 30 (時計回り）
・下向き 10kN の力により 10 × 5.0 = 50 (時計回り）

・R_B により R_B × 4.0 （反時計回り）です。

モーメントの和は０なので、時計回りのモーメントの和 80 と、反時計回りのモーメント R_B × 4.0 が等しいです。従って、R_B = 20 です。ちなみに、問われていませんが （１）より、R_A = 50 もわかります。

以上より、正解は 1 です。

類題 H29 no61 等分布荷重が作用した梁
https://yaku-tik.com/koumuin/h29-gijyutu-61/