問 題
二分探索に関する次の記述の ㋐、㋑ に当てはまるものの組合せとして最も妥当なのはどれか。
「二分探索とは、昇順又は降順に並んでいるデータを対象に、データを探し出す探索法である。
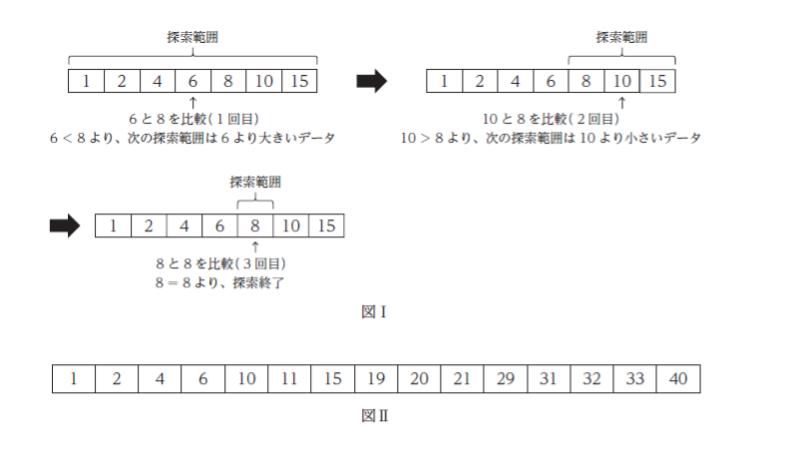
図Ⅰは、7 個のデータの中から「8」を二分探索で探す様子を示している。探索範囲の中央値と目的のデータとを比較し、一致していれば探索終了、一致していなければ、その大小関係に応じて、今回の探索範囲のうち比較対象としたデータより大きい又は小さいデータを次の探索範囲として、同様の処理を繰り返す。
図Ⅰでは、3 回の比較で探索が終了している。このような二分探索を用いて、図Ⅱのような15 個のデータから「2 」を探す場合、探索が終了するまでの比較回数は ㋐ 回である。
また、1023 個のデータから同様に二分探索でデータを探す場合、探索が終了するまでの比較回数は最小で 1 回、最大で ㋑ 回である(ただし、目的のデータは 1023 個のデータに含まれているものとする。)。」
解 説
問題文に書いてあることは、一般的な二分探索の基礎知識としてまとめておくとよいです。
【二分探索 基礎知識】
・順番に並んでるデータが対象
・「中央値と目的値のデータ比較 → 一致したら 終わり、不一致なら、大小関係に応じて探索範囲を絞り込む」という操作の繰り返しである
‐‐‐
図Ⅱにおける中央値、つまり小さい方から数えて丁度真ん中のデータは、データが 15 個なので 8 個目です。つまり「19」が中央値です。探しているのは「2」なので 19 > 2 です。そのため、19 よりも小さな7個のデータに注目して、改めて考えます。
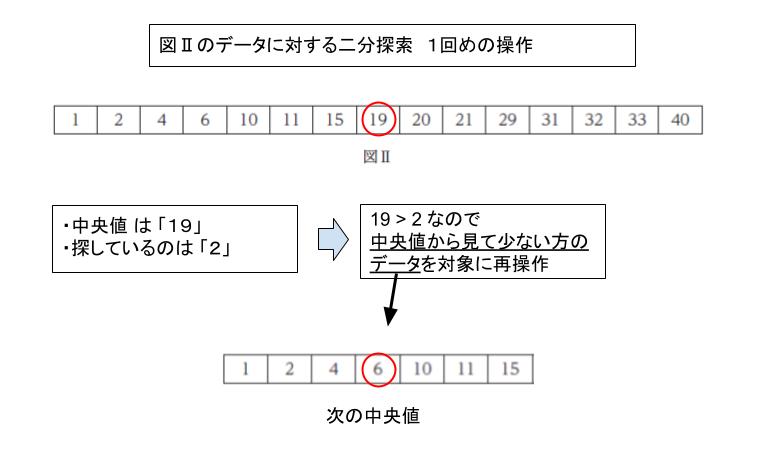
次のデータの中央値は6で 6>2 なので、また小さな方の3個のデータに注目です。すると中央値が2 なので、一致します。探索終了です。比較したのは「19 > 2、6 > 2、2 = 2」の3回です。㋐ は「3回」です。
㋑ ですが
図Ⅱの探索において一番時間がかかるのは、探索する値が1や40のように端っこの時とわかるのではないでしょうか。すると、データ数 15 の時の最大探索回数が4回です。
データ数1なら1回、データ数2なら2回がありえる。データ数3なら2回、データ数4なら3回がありえる・・・と、データ数が小さい方で傾向を考えてみます。どうも 2n を境に最大探索回数は1増えるようです。
また、データ数「15」や「1023」といった、あからさまに 2n ー 1 のデータ数をヒントにすると、データ数 2n ー 1 の時、最大 n 回と推測できるのではないでしょうか。1023 は 210 -1なので、最大10回と考えられます。㋑ は「10」です。
以上より、正解は 4 です。

コメント