問 題
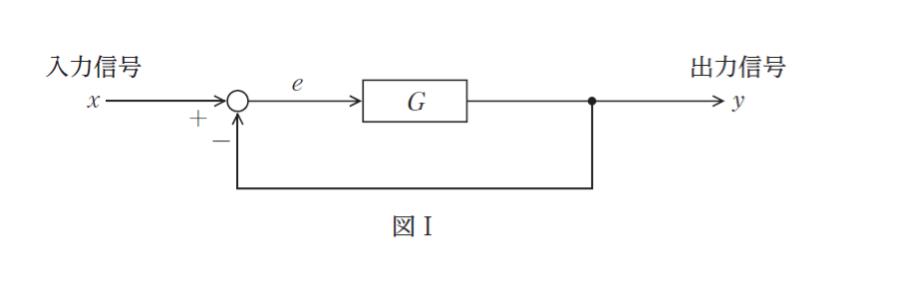
図Ⅰのブロック線図において、各部の信号は式 ①、② のように表される。
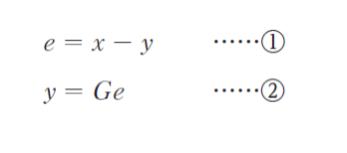
式 ① に式 ② を代入して e を消去し整理すると、図Ⅰのブロック線図の伝達関数 y/x は式 ③ のように求めることができる。
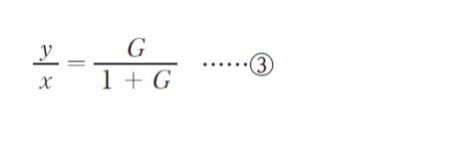
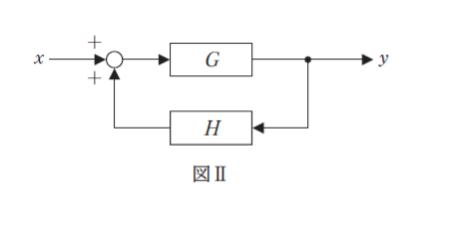
図Ⅱのブロック線図の伝達関数 y/x として最も妥当なのはどれか。なお、図Ⅰと違い、フィードバック信号と入力信号とが加算されていることに注意すること。
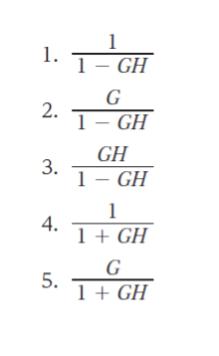
解 説
【図Ⅰの伝達関数の求め方】
図Ⅰのブロック線図における式変形をふまえて考える問題です。まず、図Ⅰの 伝達関数が、どのような式変形でできるかを以下で示します。

【図Ⅱの伝達関数の求め方】
図Ⅱにおいて、白丸(加合わせ点)の少し右部分の信号を u とおきます。G を通過すれば Gu となります。Gu は2手に分かれ、H を通過した部分を f とおくと、f = GHu になります。u = x + f です。以下の図のように、各部分の信号を表すことができます。
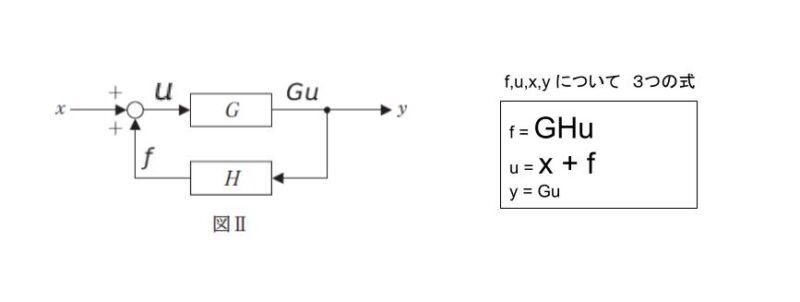
やや複雑な式変形になるのですが、3つの式から y/x を出すと、G/1-GH です。正解は 2 です。
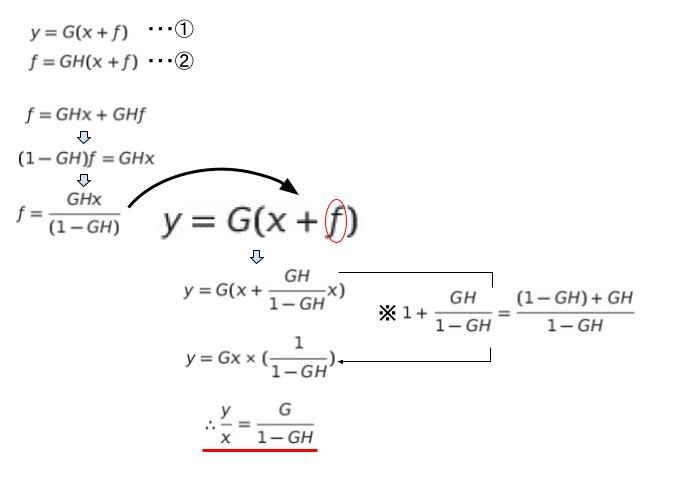
別解
都合のいい具体的な数を考えます。H = 0 とした時、単純に G を通しているだけなので、y = Gx で、y/x = Gx/x = G となるはずです。選択肢に H = 0 を代入すると、G になるのは 選択肢 2,5 です。
さらに、選択肢 5 の「G/(1+GH)」は、フィードバック信号を減算する 基本的なフィードバック回路の伝達関数です。(これは基礎知識です)。本問ではフィードバック信号と入力信号が加算になっているため、異なると考えられます。
以上より、正解は 2 です。
類題 2022 no28 ブロック線図
https://yaku-tik.com/koumuin/2022-gijyutu-28/

コメント