問 題
4 人が 1 列に並ぶとき、特定の 2 人が隣り合う確率はいくらか。
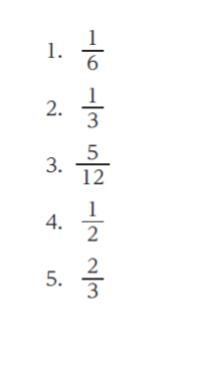
正解 (4)
解 説
確率の定義は「該当する通り/全ての通り」です。4人が1列にならぶ 全ての通り は 4 × 3 × 2 × 1 = 24 通りです。樹形図で全てあげられるようにしておきましょう。左端が A の場合が以下の通りです。
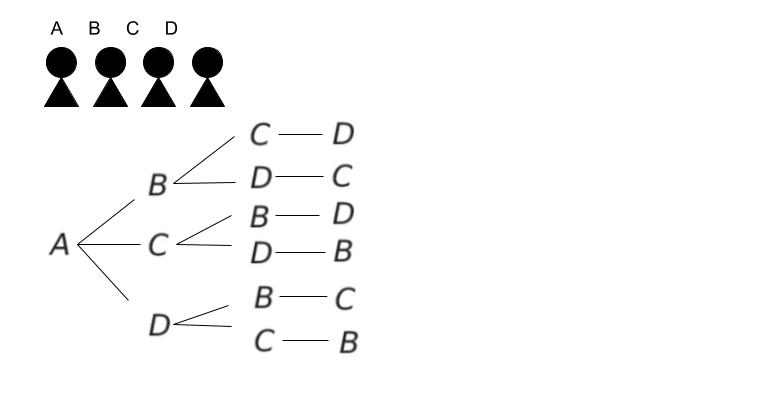
次に該当する通りを考えます。
特定の2人(例えば AB のペア)をひとまず紐でがっちり縛って1人とみなして考えます。4人ですがある2人をがっちりしばっているので「全部で3人の並び方」と見れば 3×2×1=6 通り、特定の2人が隣り合う場合を見つけることができます。
左端が AB、及び C の場合が以下の通りです。D の場合はぜひ考えてみてください。
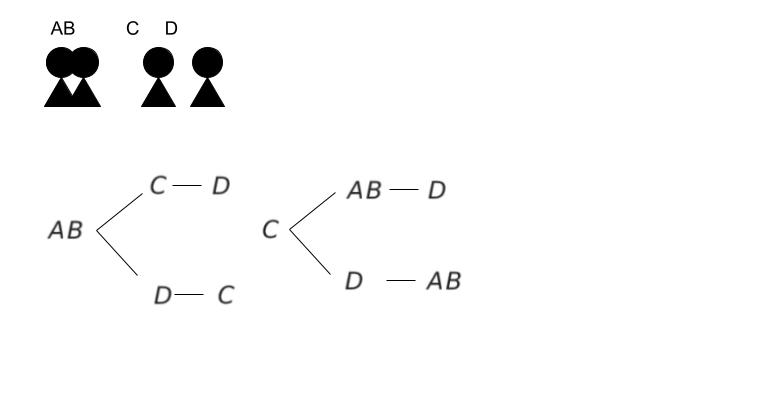
そして、縛った2人の左右は入れ替え可能なので2倍します。 「6 × 2 = 12通り」 が 該当する通り です。求める確率は 12/24 = 1/2 です。
以上より、正解は 4 です。
類題 2022 no9 確率
https://yaku-tik.com/koumuin/2022-gijyutu-09/

コメント