問 題
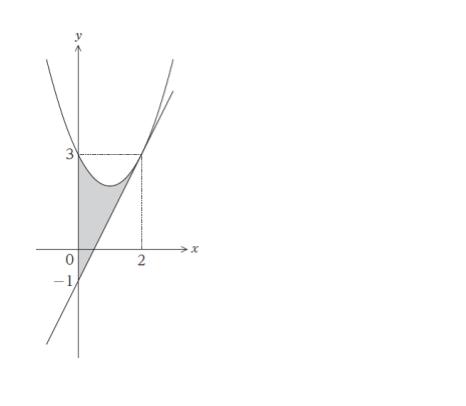
放物線 y = x2 -2x+ 3、この放物線上の点(2,3)における接線 y = 2x – 1 及び直線 x = 0 で囲まれる部分の面積はいくらか。
正解 (2)
解 説
【解法1:定積分による計算】
斜線部の面積は、上端が y = y = x2 -2x+ 3、下端が y = 2x – 1 なので、以下のような定積分で表せます。計算すると 8/3 です。以上より、正解は 2 です。
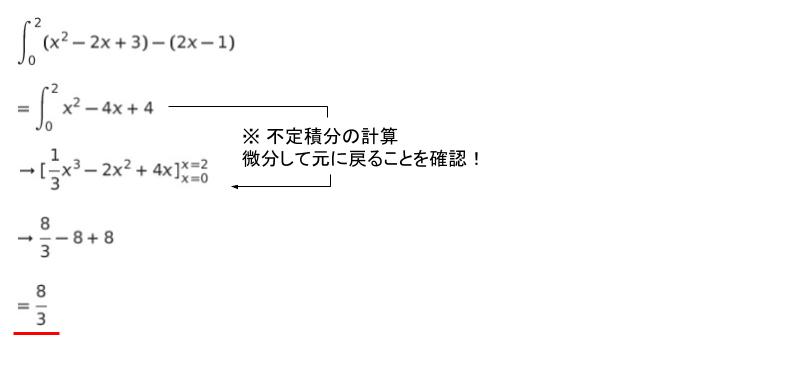
※積分が苦手なら避けた方がよい印象です。
【解法2:選択肢を活用、概算】
以下のように概算します。
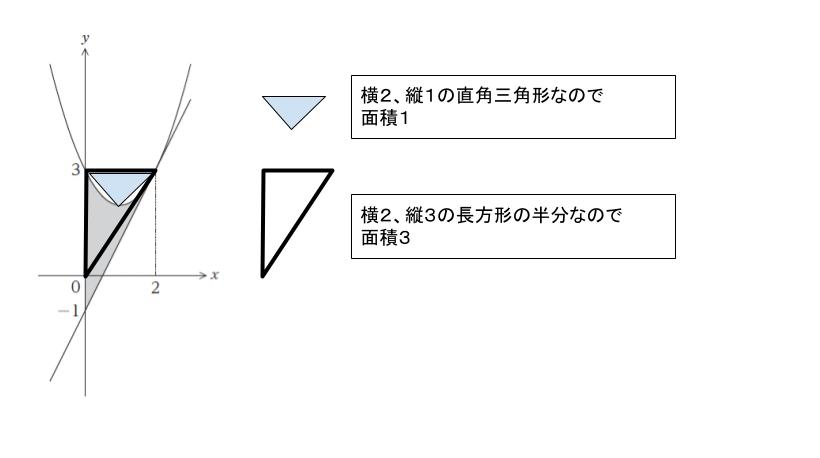
斜線部の面積は
「面積3の直角三角形から少しえぐって、少し下にはみ出し部分がある」といえます。またえぐっている部分を直角三角形とみなせば、大体面積1です。従って、面積は「3-1」よりも少し大きいため、面積2~3と概算できます。満たす選択肢は 2 です。
以上より、正解は 2 です。
類題 2022 no8 曲線で囲まれた領域の面積
https://yaku-tik.com/koumuin/2022-gijyutu-08/

コメント