公務員試験 2023年 国家一般職(土木) No.29 解説

　問 題　　　　　

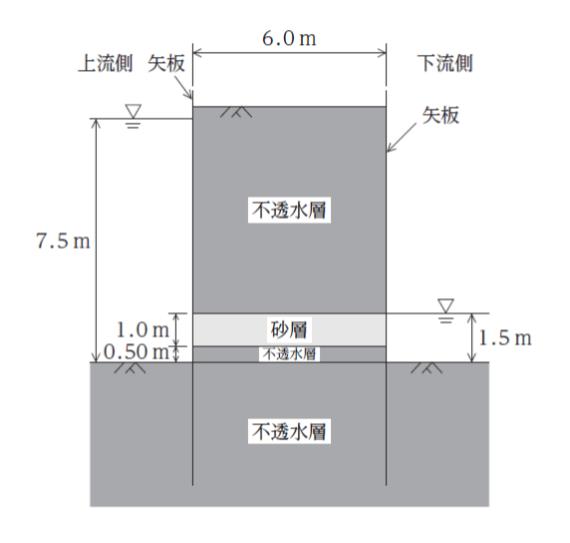
図のような幅 6.0 m の矢板の仮締切り堤の下端から 0.50 m のところに、厚さが 1.0 mで透水係数が 3.0 × 10^-3 cm/s の砂層があり、そこを通って漏水している。上流側と下流側の水位が図のようなとき、砂層を通って1日に漏水する単位奥行き (1.0 m) 当たりの水の量として最も妥当なのはどれか。

ただし、矢板は自由に透水するものとする。また、上流側と下流側の水位は変化せず、砂層以外は不透水層とする。

1． 2.6 m³
2． 2.8 m³
3． 3.0 m³
4． 3.2 m³
5． 3.9 m³

 

 

 

 

 

　解 説　　　　　

土中の水の流れなので「ダルシーの法則」を思い出します。v = ki です。ここで i は「動水勾配」です。i = Δh/Δl です。「水頭差」を「透水層の長さ」で割ったものが i です。本問における動水勾配は (7.5 – 1.5)/6.0 = 1.0 です。

v = ki で i = 1.0 なので、v = k = 3.0 × 10^-3 cm/s です。問われているのは水の量なので、Q = Av を思い出します。単位奥行き当たりであれば、表面積は 1 × 1 = 1 m² です。単位に注意して、Q = 1 × 3.0 × 10^-5 m³/s となります。

1 秒で 3.0 × 10^-5 だから
1 日 = 86400 秒で 8.64 × 10⁴ × 3.0 × 10^-5 ≒ 2.6 m³/日 です。

以上より、正解は 1 です。

類題 2021 no29
https://yaku-tik.com/koumuin/2021-doboku-29/