問 題
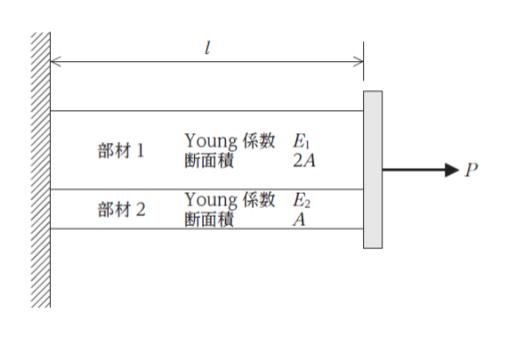
図のように、それぞれ一様な弾性体で材質と断面積の異なる 2 種類の部材 1 、部材 2 の片端が壁に固定されている。もう一方の端部に剛板を取り付け、両部材の伸びが等しくなるように引張力 P を作用させた。このとき、両部材の伸び量 Δl として最も妥当なのはどれか。
ただし、P を作用させる前の部材 1 、部材 2 の長さは l、Young 係数はそれぞれ E1,E2、断面積はそれぞれ 2A,A、断面形状はそれぞれ一様とする。また、各部材の自重及び引張りに伴う断面積の変化は無視できるものとし、各部材は軸方向のひずみが断面内で均一になるものとする。
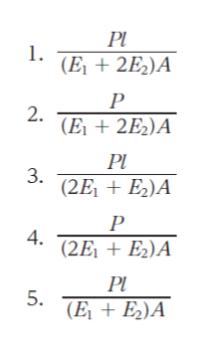
正解 (3)
解 説
【ひずみに関する基礎知識】
力を加えて、元々 長さ l の物体が Δl 伸びた時、ひずみ ε を Δl/l で表します。この時、E をヤング係数(ヤング率)として、σ = Eε が成立します。σ は軸応力です。軸方向力を P、断面積 A とすると、軸応力 σ は P/A です。

本問では、軸方向のひずみが均一なので
部材 1 について 、ひずみ ε1、軸応力度 P1/2A
部材 2 について、 ひずみ ε2、軸応力度 P2/A とすると
ε1 = (P1/2A)/E1 ・・・(1)
ε2 = (P2/A)/E2 ・・・(2)
と表せます。そして、ε1 = ε2 = Δl/l です。また、P1 + P2 = P です。
(1) より
(Δl/l) × 2AE1 = P1 … (3)
(2) より
(Δl/l) × AE2 = P2 …(4)
(3) + (4)
(Δl/l) × A × (2E1 + E2) = P
∴ Δl = (P × l) / A(2E1 + E2)
以上より、正解は 3 です。

コメント