公務員試験 2023年 国家一般職(土木) No.22 解説

　問 題　　　　　

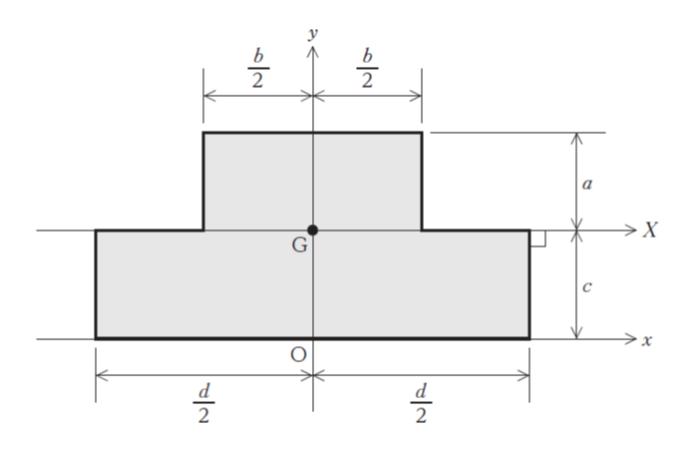
図のような xy 平面 (直交座標系) における長方形形状を組み合わせた断面の寸法のうち、a、b、d が定められている場合に、網掛けで表わされた図形の図心 G が X 軸上にあるための c の値として最も妥当なのはどれか。

 

 

 

 

 

　解 説　　　　　

上の小さな長方形と、下の大きな長方形に分けて考えます。長方形の図心は「対角線の交点」です。それぞれ A、B とおきます。

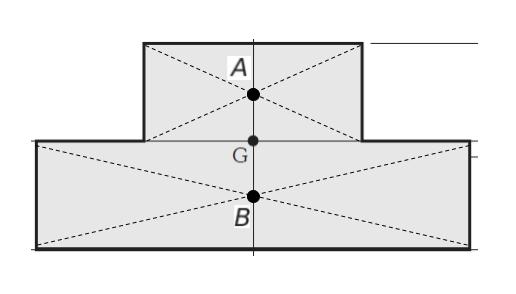
線分 AB に注目し、ちょうど釣り合いの点が G となればよいです。端 A には 横 b、縦 a の長方形の面積 ab、端 B には 横 d、縦 c の長方形の面積 cd が重りとして吊り下がっているとみなします。すると、AG：GB = cd：ab が成立すればよいです。

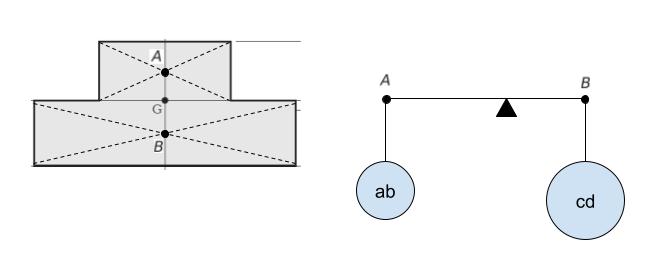
また、図から明らかに
AG = a/2、GB = c/2 です。

従って
a/2：c/2 = cd：ab
→ a：c  = cd：ab
→ a²b = c²d です。後は c について解きます。

c² = a²b/d

∴ c = a√(b/d) です。

以上より、正解は 5 です。