問 題
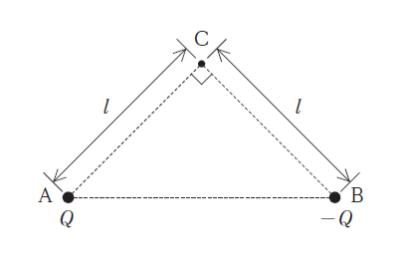
図のような ∠ACB = 90° の直角二等辺三角形 ABC があり、辺 AC 及び辺 BC の長さは共に l である。点 A に電気量 Q (Q > 0)、点 B に電気量 -Q の点電荷をそれぞれ置いたとき、点 C における電場の強さとして最も妥当なのはどれか。ただし、クーロンの法則の比例定数を k とする。
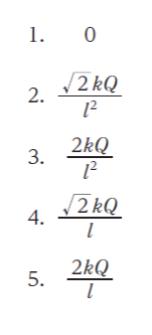
正解 (2)
解 説
【点電荷が作る電場】
点電荷が出てきたら、まずはクーロンの法則です。これは、2つの点電荷がありそれぞれが Q1,Q2 の電荷を持つ時に「F = kQ1Q2/r2」 の力がそれぞれの電荷に働くという法則です。
ある点電荷をおくことで空間の性質が変化し「その空間に電荷を置くと力が発生するようになった」と考えることで空間を「電場(電界)」と呼んだりします。
「ある点における電場(電界)の強さ」の定義を「ある点に1Q の点電荷を置いた時にその1Q の点電荷に働く力の強さ」とします。その力は、クーロンの法則のうち1 つの電荷を 「1」とおけばわかります。 つまり、kQ/r2 です。
点 A、B 各点における点電荷が作る電場の大きさが kQ/r2 です。1Q の点電荷を C においたと考えれば、点 A においた点電荷とは「斥力」、点 B においた点電荷とは「引力」が作用します。以下の図のようにまとめられます。点 C における電場の大きさは √2 kQ/l2 です。
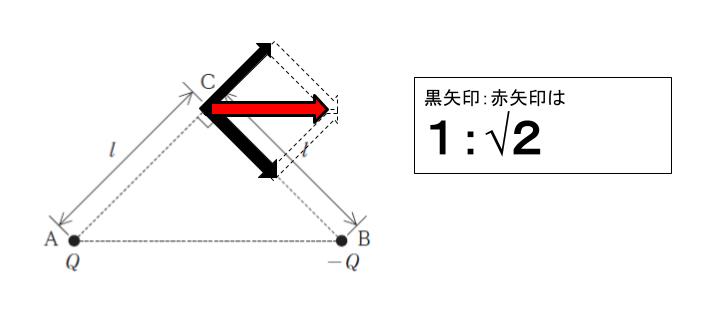
以上より、正解は 2 です。
類題 H24 no18
https://yaku-tik.com/koumuin/h24-doboku-18/

コメント