問 題
ある放射性原子核の半減期が 25 日であるとき、初めに存在した原子核の数が 1/6 になるのに要する日数として最も妥当なのはどれか。
ただし、log10 2 = 0.30、log10 3 = 0.48 とする。また、初めに存在した原子核の数を N0、半減期を T、経過時間を t とすると、未崩壊の原子核の数 N は、
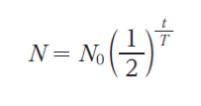
で与えられるものとする。
1. 58 日
2. 60 日
3. 63 日
4. 65 日
5. 68 日
正解 (4)
解 説
半減期は、半分になるまでの時間です。25 日 で 1/2、50 日で 1/4、75 日で 1/8 ということです。50 ~ 75 日のどこかで 1/6 になります。
【解法 1:グラフの概形を書き、選択肢を評価】
できるだけ正確に 縦軸として 0.5、0.25、0.125 をとります。1/6 は 0.16… です。以下のようにグラフの概形を書けます。
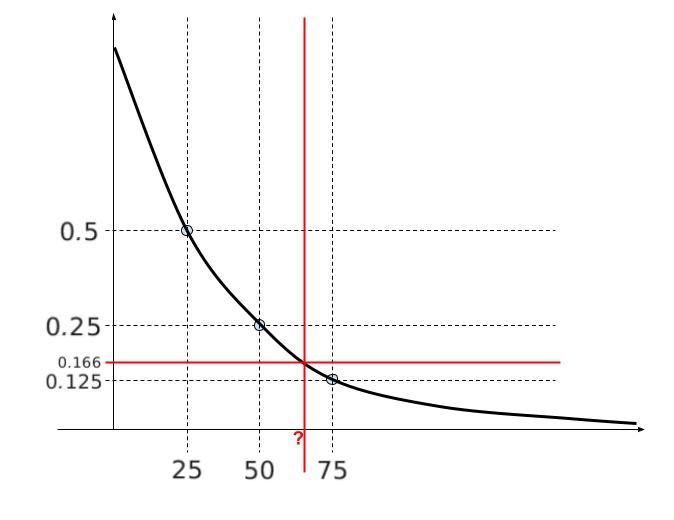
50 と 75 の中間である 62.5 よりも少し右、さらに 62.5 と 75 の中間付近 68.75 よりはやや左 と読み取れると思われます。選択肢から 65 日が妥当です。
以上より、正解は 4 です。
【解法 2:与えられた式の利用】
N = N0/6、T = 25 を代入します。両辺を N0 で割れば 1/6 = (1/2)t/25 です。ただしのヒントも参考に、両辺の対数を、底 10 でとります。以下のように変形すれば、t = 65 です。
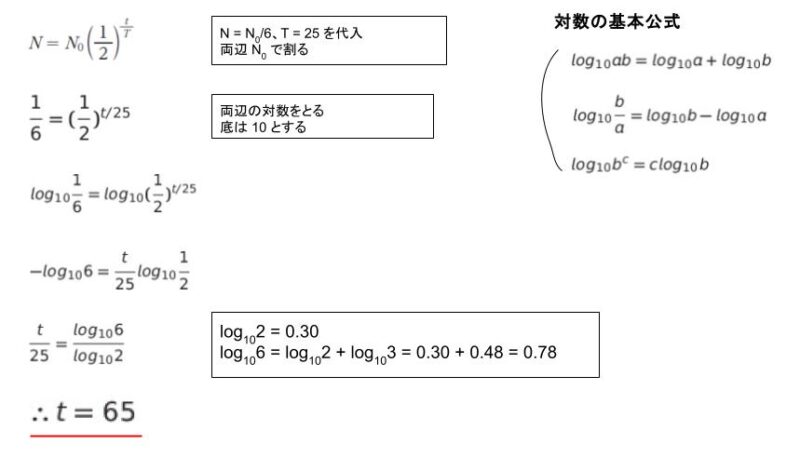
以上より、正解は 4 です。

コメント