問 題
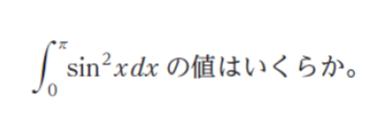
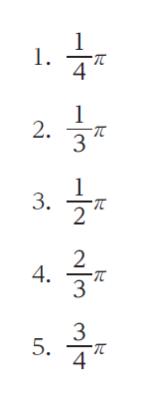
正解 (3)
解 説
積分で解いたことがあれば、sin2x = (1-cos2x)/2 と変形して積分でよいです。知らなかった場合にも、グラフの概形を書いて、具体的に考えたい問題です。
※ π ≒ 3.14 です。
※ π(ラジアン) = 180° です。
【グラフの概形から概算】
y = sin2x とおきます。
・x = 0 の時、y = 0 です。
・x = π/4 の時、y = 1/2 です。
ちなみに、y = sinx であれば、x = π/4 の時、y = √2/2 ≒ 0.7
・x = π/2 の時、y = 1 です。
点を滑らかにつなぎグラフの概形を考えます。また、参考のため、y = sin x のグラフも書き込んでいます。
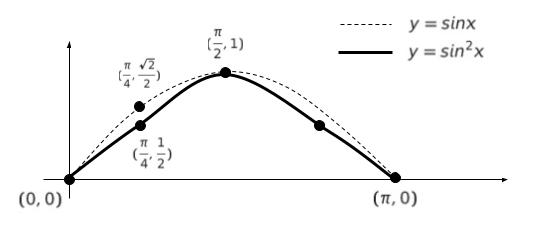
y = sin2x のグラフと x 軸で囲まれる面積を 三角形で概算すれば「底辺 π、高さ 1 の三角形」です。面積が π/2 です。
以上より、正解は 3 です。
【積分で計算】
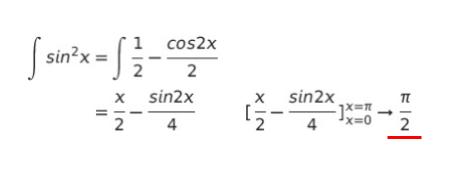
以上より、正解は 3 です。

コメント