公務員試験 2023年 国家一般職(土木) No.3 解説

　問 題　　　　　

xy 平面上において、曲線 y = x³ + kx² + 2x + 4 上の x = 1 の点における接線が原点を通るとき、定数 k の値はいくらか。

1．-2
2．-1
3． 0
4． 1
5． 2

 

 

 

 

 

　解 説　　　　　

接線が問われている → 微分　が定石です。

y = x³ + kx² + 2x + 4…(1)
y’ = 3x² + 2kx + 2 です。x = 1 を代入すれば 2k + 5 となります。この値「2k + 5」が「x = 1 における接線の傾き」です。

また、(1) に x = 1 を代入すれば、y = k + 7 です。グラフは 点 (1,k+7) を通ります。

従って
点 (1,k+7) における接線を考えると　傾きが 2k+5 である。傾き 2k + 5 である、x = 1 における接線が原点 (0,0) を通ればよいという問題です。

ここまででわかったことをグラフで表すと、以下のようにまとめることができます。

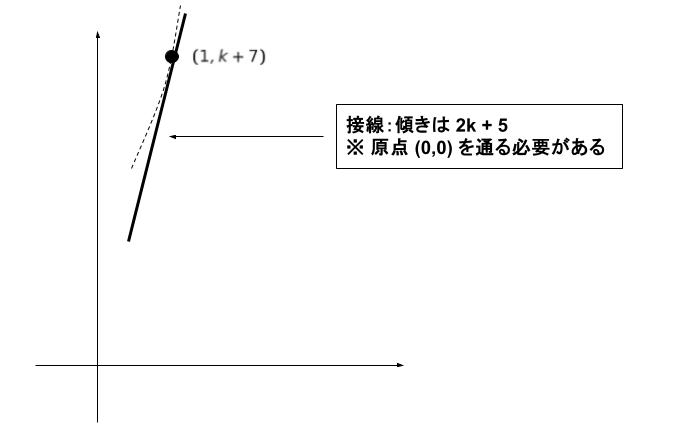
選択肢 から 具体的に考えると

k = -2
→ 接線の傾きが 1 となり、明らかに原点を通りません。

k = -1
→ 接線の傾きが 3、(1,6) なので、x = 0 の時 y = 3 です。原点通りません。

k = 0
→  接線の傾きが 5、(1,7) なので、x = 0 の時 y = 2 です。原点通りません。

k = 1
→ 接線の傾きが 7、(1,8) なので、x = 0 の時 y = 1 です。原点通りません。

選択肢 1 ~ 4 まで誤りです。

以上より、正解は 5 です。