公務員試験 2023年 国家一般職(土木) No.1 解説

　問 題　　　　　

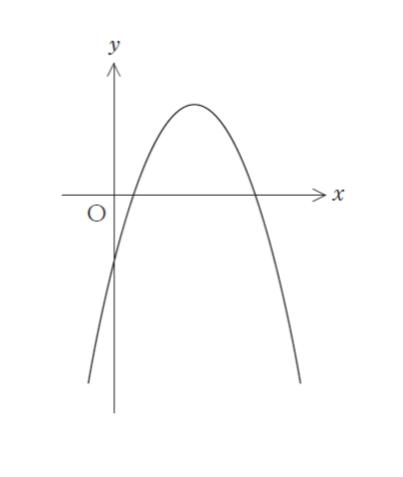
2 次関数に関する次の記述の ㋐、㋑、㋒ に当てはまるものの組合せとして正しいのはどれか。

「y = ax² + bx + c のグラフが図のようになるとき、b は ㋐、b² – 4ac は ㋑、a – b + c は ㋒ となる。」

 

 

 

 

 

　解 説　　　　　

・グラフの形が上に凸 なので a < 0 です。

・頂点の x 座標である 軸は x = -b/2a です。これは基礎知識です。忘れていても 平方完成して y = a(x + b/2a)² +… と変形すれば導くことができます。

グラフから「軸の符号は 正」です。
式で書けば 「-b/2a > 0」です。a < 0 なので b > 0 です。

不等式でわかりにくければ、適当な数字で考えればよいです。
例えば a = -1 とすれば -b/-2 > 0 となる場合
b の符号は 正でなければならない　ということです。

㋐ は「正」です。正解は 1 ~ 3 です。

・頂点の座標が (-b/2a、-(b²-4ac)/4a) です。基礎知識として暗記しているか、平方完成で導きます。頂点の y 座標がグラフより 正です。a < 0 なので、b² – 4ac > 0 です。㋑ は「正」です。正解は 1 or 2 です。

・x = -1 の時、y 座標が a – b + c です。明らかにグラフより負です。㋒ は「負」です。

以上より、正解は 2 です。

【別解】具体的なグラフを見つける

上に凸なので、y = -x² を考えます。もう少し頂点が右上なので、頂点の候補として (1,1) として y =  -(x – 1)² + 1 を考えます。x = 0 の時 y = 0 になってしまうので、少し下に下げれば OK です。頂点 (1,1/2) → y = -(x – 1)² + 1/2 ＝ -x² + 2x – 1/2 が一例として見つかります。

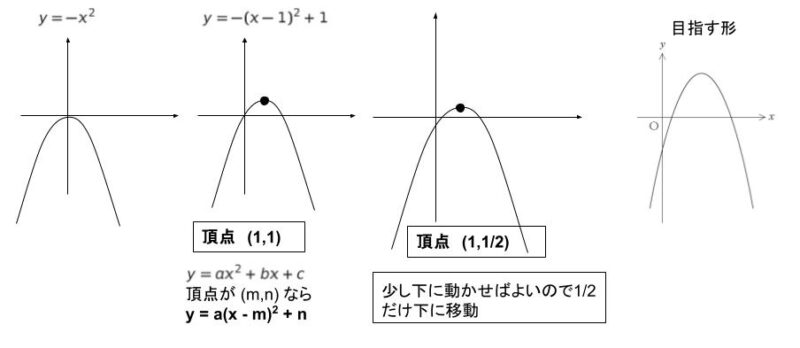
この時、a = -1、b = 2、c = -1/2 です。

従って
b は正、b²-4ac = 4 – 2 なので 正、a – b + c = -1 -2 – 1/2 なので負です。

以上より、正解は 2 です。