問 題
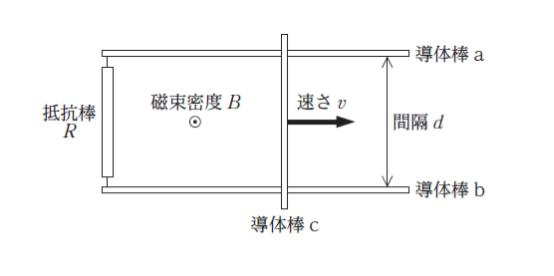
図のように、紙面に垂直上向きで磁束密度 B の一様な磁界の中に、紙面と平行な面上に抵抗値 R の抵抗棒と、導体棒 a と b が置かれている。a と b は間隔 d で平行に配置され、左端に抵抗棒がつながれている。導体棒 c は、a と b に直交して接した状態のまま、右向きに一定の速さ v で移動している。
このとき、抵抗棒で消費される電力として最も妥当なのはどれか。ただし、a,b,c の抵抗は無視できるものとする。
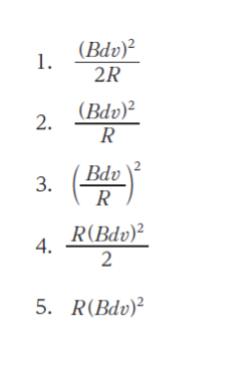
正解 (2)
解 説
磁場を横切る導線が動いているので、誘導起電力 V = vBd が生じます。これは基礎知識です。
キルヒホッフの法則より「起電力の和=電圧降下の和」です。左辺 V = vBd、右辺 RI を代入することで vBd = RI・・・(1) を得ます。
電力 P = VI = RI2 です。選択肢を見ると I を消去すればよいとわかります。(1) を I について解けば I = vBd/R となります。従って、P = R(vBd/R)2 = (vBd)2/R です。
以上より、正解は 2 です。
類題 H26 no23
https://yaku-tik.com/koumuin/h26-denjyou-23/

コメント