問 題
ある値の近似値をニュートン法を応用して求めることを考える。ニュートン法は、関数 f (x) を方程式 f (x) = 0 のある近似解 xn のまわりにテイラー展開した下式について、左辺を 0 、右辺第 3 項以下を 0 とした方程式の解 x を新たな近似解 xn+1 とし、xn+2,xn+3,…を繰り返し計算することにより、方程式 f (x) = 0 の近似解を求める方法である。
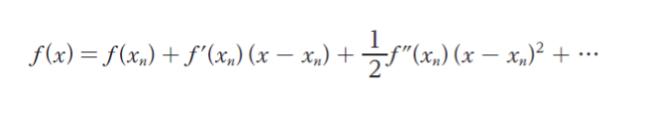
いま、この方法を応用して 4√a の近似値 (ただし、a > 0) を求める。i 番目の近似値を xi としたとき、xi+1 を xi で表した式として最も妥当なのはどれか。
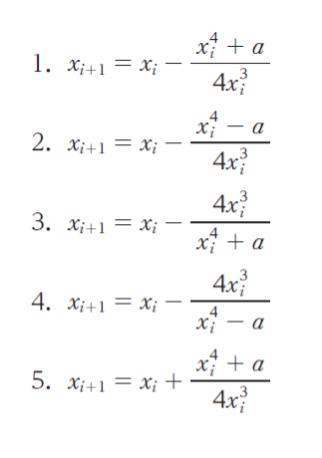
解 説
4√a の近似値を考えるため、f(x) = x4 – a を考えます。 f(x) = 0 を解くと x = 4√a になりますね。微分すると f'(x) = 4x3 です。
問題文の式を指定により「左辺 0、右辺 第 3 項以上を 0」とすると「0 = f(xn) + f'(xn)(x-xn)」・・・(1) です。ここで注意して見てほしいのは、この右辺ごちゃごちゃしているけど「1 次式」という点です。f (xn)、f'(xn) は 1.12 といった具体的数を表しています。
つまり、(1) 式は △、▢ を 定数として「0 = △ + ▢ x – ▢」という式です。そのため、x = … という形にして解けます。計算過程は以下の通りです。
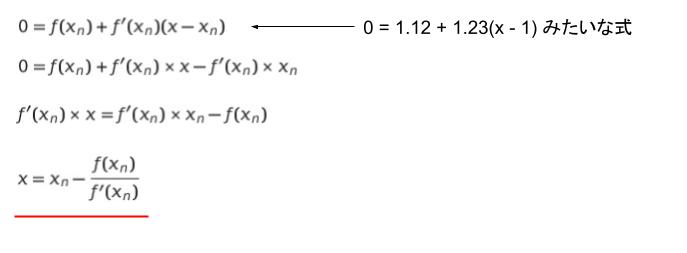
選択肢に合わせて n を i とします。上の式変形の結果出した x というのが新たな近似解なので xi+1 です。f(x) = x4 – a、f'(x) = 4x3 であることから、選択肢より 答え を選べると思われます。
以上より、正解は 2 です。
類題 H29 no35 ニュートン法
https://yaku-tik.com/koumuin/h29-denjyou-35/

コメント