問 題
A、Bの 2 人がそれぞれ自動車を使って地点 X を出発し、地点 Y を経由して、地点 Z にその日のうちに到着した。次のことが分かっているとき、区間 XY 及び区間 YZ のそれぞれの距離の和はいくらか。ただし、各人は各区間をそれぞれ一定の速さで移動していたものとする。
○ A は午前 10 時 00 分に地点 X を出発し、区間 XY を時速 40 km で移動し、地点 Z に午前 11 時 45 分に到着した。
○ B は午前 9 時 00 分に地点 X を出発し、区間 YZ を時速 30 km で移動し、地点 Z に午前 11 時 30 分に到着した。
○ 区間 XY の距離は、区間 YZ の距離の半分であった。
○ 区間 YZ における A の速さは、区間 XY における B の速さと同じであった。
1.80 km
2.90 km
3.100 km
4.110 km
5.120 km
解 説
箇条書きの条件を上から条件1、条件2・・・とします。文章題で、一読してイメージがわかない問題はまず図示です。図示の一例が以下のようになります。条件3をふまえ、XY の距離と YZ の距離を大体1:2として描くとよいです。
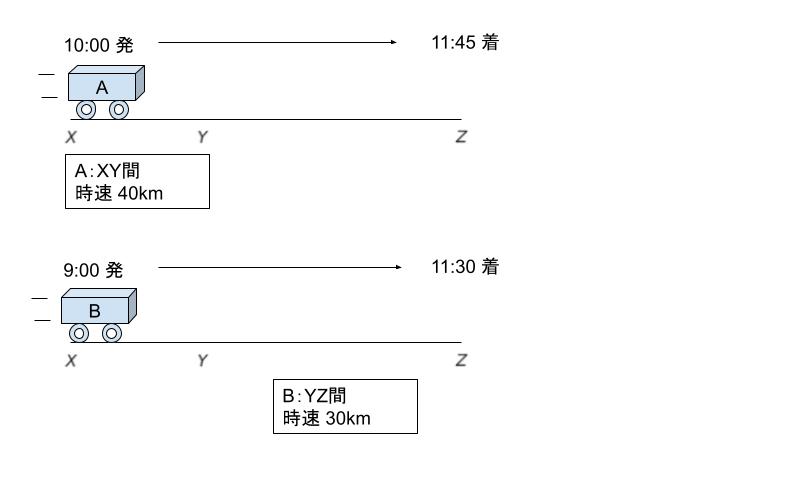
XY:YZ = 1:2であることから、和が3の倍数の時、それぞれきれいな整数になります。選択肢の値の中で3の倍数は 90、120 です。そこでまず小さい方の値である選択肢 2 を正解と仮定します。XY = 30km、YZ = 60km と仮定するということです。
「A:XY 間 かかる時間」は 30/40 = 3/4 時間 = 45 分です。すると、到着が 11:45 なので YZ 間を 1 時間で移動したことになります。「A :YZ 間 速さ」は 60 ÷ 1 = 60 なので、時速 60km とわかります。問題文より、 B の XY 間の速さも 時速 60km です。
「B:XY 間 かかる時間」は 30/60 = 1/2 時間 = 30 分です。YZ 間は 60 ÷ 30 = 2 時間です。全体で 2.5 時間かかるので、問題文と矛盾ありません。これが正解です。
以上より、正解は 2 です。
—
【別解 文字を使って表す ※おすすめしません 複雑です。でも文字での計算が好きな人は、こちらの方がいいかもしれません】
XY 間を x km とけば、YZ 間が 2x km と表せます。
A に注目すると、XY 間 かかった時間が x/40 です。1 時間 45 分 = 7/4 時間 = 70/40 時間なので、YZ 間 かかった時間が (70-x)/40 と表せます。
速さ = 道のり ÷ かかった時間 なので、A の YZ 間の速さは 2x ÷ (70-x)/40 = 80x/(70-x) です。これが B の XY 間の速さでもあります。
すると、B の XY 間 かかった時間は x ÷ 80x/(70-x) = (70-x)/80・・・(1)です。YZ 間 かかった時間は 2x/30・・・(2)です。(1)+(2)= 2.5 となるような x を解くと x = 30 です。そのため、XY = 30km、YZ = 60km で、合計 90km となります。

コメント