問 題
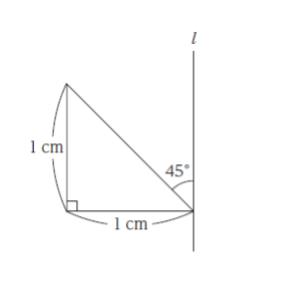
図のように、直角二等辺三角形を直線 l を軸として1 回転させたときにできる立体の体積として正しいのはどれか。
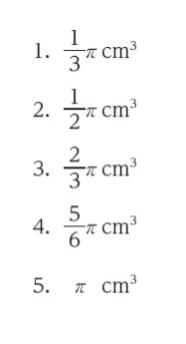
正解 (3)
解 説
軸から離れた部分があると、回転させた時に複雑になります。そのため「軸にくっついている正方形の回転体」ー「軸にくっついている直角三角形の回転体」として考えるとよいです。
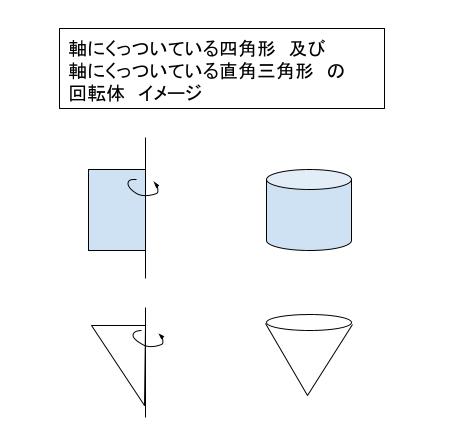
円柱の体積は「底面積 × 高さ」です。円錐の体積は「底面積 × 高さ × 1/3」です。底面積は共に半径1の円なので、共に π です。円柱の体積が π × 1、円錐の体積が π × 1 × 1/3 となります。
従って、求める体積は
πーπ/3
= 2π/3 です。
以上より、正解は 3 です。

コメント