問 題
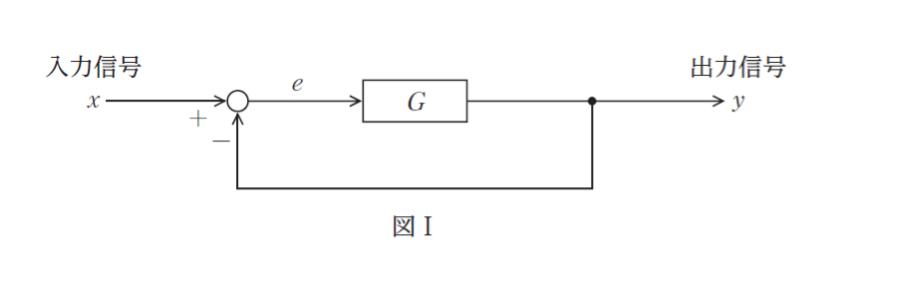図Ⅰのブロック線図において、各部の信号は式 ①、② のように表される。
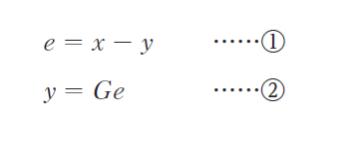
式 ① を式 ② に代入して e を消去すると、図Ⅰのブロック線図の伝達関数 y/x は式 ③ のように表される。
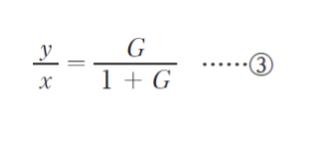
このとき、図Ⅱのブロック線図の伝達関数 y/x として最も妥当なのはどれか。
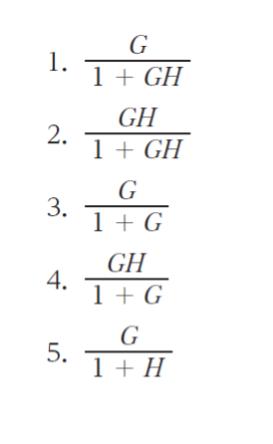
解 説
【図Ⅰの伝達関数の求め方】
図Ⅰのブロック線図における式変形をふまえて考える問題です。まず、図Ⅰの 伝達関数が、どのような式変形でできるかを以下で示します。
【図Ⅱの伝達関数の求め方】
図Ⅱでは y = Gu = G(x – f)・・・（１） となることが、図より読み取れます。また、f = Hu = H(x – f)・・・（２） です。
（２）を使って （１）の f を消去することで伝達関数を求めます。以下のように変形します。
以上より、正解は 5 です。
別解：正解が見つかるわけではないのですが、２択までは絞れます。また、少し考察すれば、なんとか正解も見つけられます。最悪２択でもいいかなと思われます。
上が G1 のみ、下が G2 のみのフィードバック系の伝達関数は、基本知識です。y/x = G1/(1+G1G2) です。
図Ⅱの回路において、G = 1 とします。すると基本知識のフィードバック系における G1 = 1、G2 = H の場合になります。この伝達関数は基礎知識より 1/1+H です。
選択肢において、G = 1 とすると、1/1+H となるのは、選択肢 1 or 5 です。これで２択となります。
さらに考察すると、『G の手前までの伝達関数が 1/1+H である』といえるのだから、最後に G が入れば G をかければよいのでは？と考えて G/1+H を選べるのではないでしょうか。
以上より、２択の段階で 1 or 5、正解は 5 です。
コメント