問 題
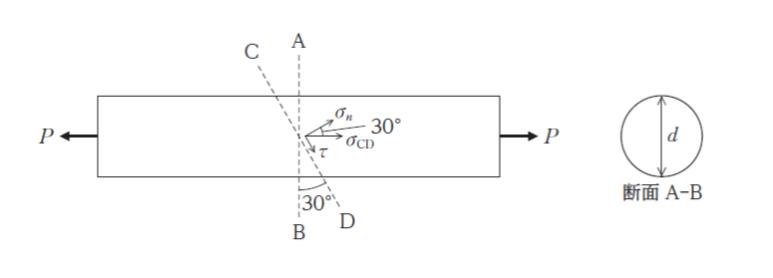
図のような直径 d の丸棒の両端に引張荷重 P が作用しているとき、P に垂直な断面 A ‒ B から 30°傾いた断面 C ‒ D には応力 σCD が生じる。このとき、断面 C ‒ D に垂直な方向の応力 σn とせん断応力 τ の大きさの組合せとして最も妥当なのはどれか。ただし、丸棒は均質で、断面は長さ方向に一様とする。
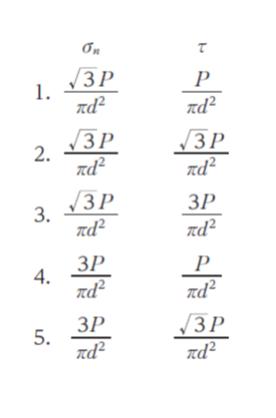
正解 (5)
解 説
※本問における θ は、公式の θ ではない。
公式では「軸力方向と斜面のなす角」を θ とする。
斜断面上の応力の公式として
・σn = σ sin2θ
・τ = (1/2) × σ sin2θ を覚えておけばよいのですが、過去問で未出のテーマであり、準備しておくのは難しかったと思います。そこで選択肢の活用を考えます。
明らかに問題文の図から、σn :τ = √3:1 に見えるのではないでしょうか。選択肢の中で、τ の √3 倍 が σn になっているのは、選択肢 1 と 5 だけです。この 2 択にしぼりたい問題です。
ちなみに
CD で切断すると (ちくわを真っ直ぐ切る場合と、斜めに切る場合を想像するとわかりやすいかもしれません)
・切断面が 円 → 楕円になる。長軸が 2/√3 倍になるから、面積も 2/√3 倍になる。※短軸の長さは変わりません。面積が 2/√3 倍になれば、応力は √3/2 倍になると考えられる。
・軸応力を CD に垂直方向に分解すれば √3/2 倍になる
従って
AB で切断した時の円の面積を A とおき、求めたい応力 σn は
σn = P/A × (√3/2) × √3/2
= P/(πd2/4) × 3/4
= 3P/πd2 ではないか、と推測できます。
以上より、正解は 5 です。

コメント