問 題
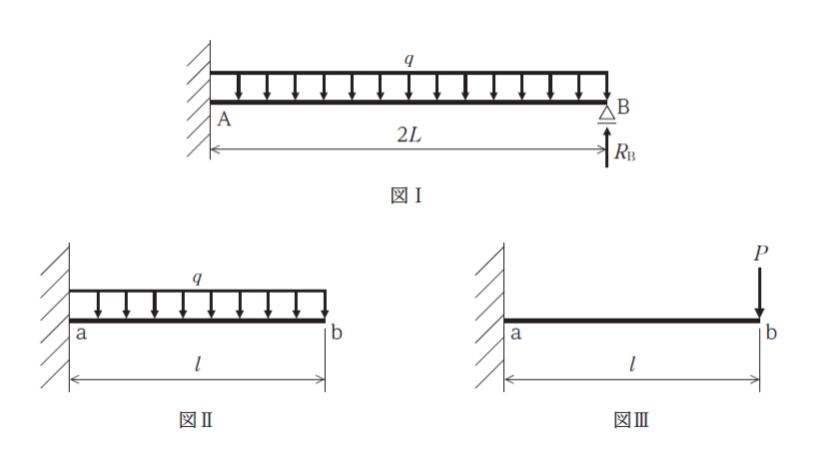
図Ⅰのような、全長に等分布荷重 q を受ける長さ 2L の片持ち梁の自由端 B が移動支持によって支えられている梁の支点反力 RB として最も妥当なのはどれか。
なお、図Ⅱのような、全長に等分布荷重 q を受ける長さ l の片持ち梁の自由端 b におけるたわみ σb1 は式 ①、図Ⅲのような、長さ l の片持ち梁の自由端 b に鉛直下向きの集中荷重 P が作用するときのたわみ σb2 は式 ② で表されるものとする。ここで、鉛直下向きのたわみを正とする。
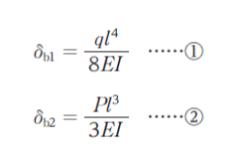
ただし、図Ⅰ、図Ⅱ、図Ⅲの断面は一様であり、Young 係数、断面二次モーメントは等しく、それぞれ、E、I とする。また、梁の自重は無視し、支点反力は鉛直上向きを正とする。
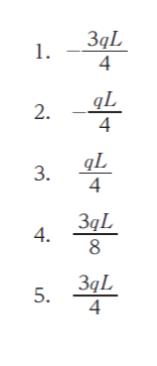
正解 (5)
解 説
見たことない問題パターンだったのではないでしょうか。図Ⅱと図Ⅲ 及び 式 ①、② が用いるべきヒントであることから「等分布荷重によって下にたわむ分」と 「RB によって上にたわむ分」が等しくなる と考えればよい問題と思われます。
【等分布荷重による下方向のたわみ】
式 ① の l に「2L」を代入します。
σb1 = 2 × qL4/EI…(1) です。
【自由端における集中荷重による上方向のたわみ】
式 ② の l に「2L」、P に RB を代入します。
σb2 = RB × (2L)3/3EI
= (8/3) × RB L3/EI…(2)
(1) = (2) なので
RB = 3/8 × 2 × qL
= (3/4) × qLです。
以上より、正解は 5 です。

コメント