問 題
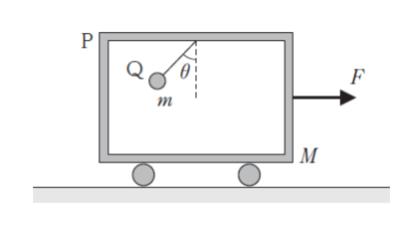
図のように、質量 M の台車 P の天井から質量 m の小球 Q を糸でつり下げ、P を滑らかで水平な床に置いた。その後、P を大きさ F の力で水平方向に引っ張ったところ、Q は糸が鉛直方向と角 θ (0 < θ < π/2) をなす位置にて、P から見て静止した。このとき、糸の張力の大きさとして最も妥当なのはどれか。ただし、重力加速度の大きさを g とする。
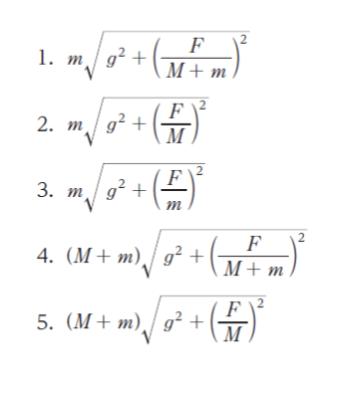
解 説
【台車 P の加速度】
F = ma より、台車 P を F で引っ張ると
F = (M+m)a より、台車 P の加速度は a = F/(M + m) です。
【小球に作用する力】
小球は下向きに mg の力が作用します。また、慣性力について F慣性 = ma より、左向きに m × F(M + m) の力が作用しているとみなせます。
【張力 T】
小球は 静止しているので力の釣り合いより、張力 T を縦方向と横方向に分解すれば
縦方向の和が 0 より、T縦 = mg…(1)
横方向の和が 0 なので、T横 = m × F(M + m)…(2) です。
張力 T = √(T縦)2 + (T横)2 です。
(1),(2) を代入し、式変形すると以下の通りです。
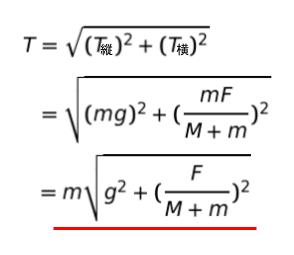
以上より、正解は 1 です。
【別解:極端な場合を考えて選択肢を消去】
・M が限りなく大きい場合、特に F の意味がなく、小球はほぼ真下に下がっていて 下向き mg の力が作用し、張力 ほぼ mg と推測できます。「M 限りなく大きいとき 張力は mg」…(1) です。
・また、m が限りなく大きい時も、特に F の意味がなく、小球はほぼ真下に下がっていて下向き mg の力が作用します。そして張力も ほぼ mg と考えられます。「m 限りなく大きい時 張力は mg」…(2) です。
選択肢 4,5 ですが
M が大きくなった時に張力が Mg になってしまうので誤りと考えられます。
選択肢 3 ですが
M によらないため、誤りと推測されます。
選択肢 1 or 2 です。
この 2 択でも十分と思いますが、更に F が大きい場合について考えます。F がとても大きく、かつ m がもっともっと大きい場合を考えてみます。この時にも mg に収束してほしいので、√ の中の F が含まれる項の分母には m が含まれるべきです。従って、選択肢 2 は誤りと考えられます。
以上より、正解は 1 です。

コメント