公務員試験 2022年 国家一般職(土木) 工学に関する基礎 No.12 解説

　問 題　　　　　

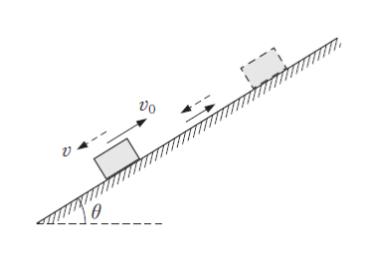
図のように、水平面と角 θ (0 < θ < π/2) をなす粗い斜面上に置かれた質量 m の小物体を、斜面に沿って上向きに速さ v₀ で滑らせたところ、小物体は最高点に到達して一旦静止した後、下向きに滑り始めた。

小物体が初めに置かれた位置に戻ってきたときの速さ vとして最も妥当なのはどれか。ただし、小物体と斜面の間の動摩擦係数を μ’ とする。

 

 

 

 

 

　解 説　　　　　

2 択までしぼれば十分な問題です。

まず、摩擦がなければ力学的エネルギー保存則より、初めの位置に戻ってきたときの速さは初速と同じ v₀ です。本問では摩擦があり、力学的エネルギー保存則が満たされないため、選択肢 1 は誤りです。

次に、μ’ = 0.5、θ = 30° と具体的に考えます。sin 30° = 1/2、cos 30° = √3/2 ≒ 0.87 です。すると選択肢 2,4 の場合 √ の中身が 1 よりも大きくなります。「摩擦力が作用する方が、速くなって戻って来る」というのはおかしいと判断できるのではないでしょうか。

従って、選択肢 3 or 5 が正解です。

ーーー
以下は補足解説です。以下のように本番で解く必要はなく、この問題に時間をかけるならば、上の解説のように 2 択までしぼれば十分と思われます。

斜面上昇中　及び　下降中における小物体に作用する力は重力と摩擦力です。図示すると以下の通りです。F_動摩擦力 = μ’ N は基礎知識です。

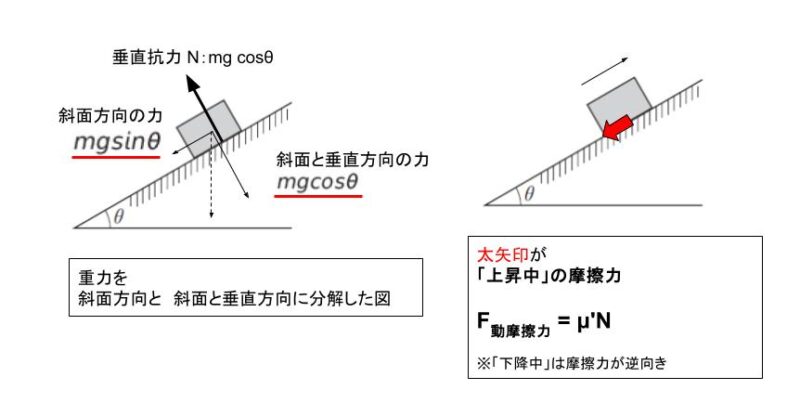
【斜面上昇中 → 停止】
斜面方向にかかる力が
-mgsinθ – μ’mgcosθ = -mg(sinθ + μ’cosθ) です。

F = ma より
-mg(sinθ + μ’cosθ) = ma です。a = -g(sinθ + μ’cosθ) です。

停止する時 v = 0 です。
v = v₀ + at なので、停止するまでにかかる時間は
t = v₀/g(sinθ + μ’cosθ)


変位 x = v₀t + at²/2
= v₀²/g(sinθ + μ’cosθ) –  v₀²/2g(sinθ + μ’cosθ)
= v₀²/2g(sinθ + μ’cosθ) だけ上昇して停止するとわかります。

※ v² – v₀² = 2ax を用いると、やや簡単に求めることができます。

【停止 → 斜面下降中について：初速 0】
斜面方向にかかる力が
mgsinθ – μ’mgcosθ = -mg(-sinθ + μ’cosθ) です。

F = ma より
-mg(-sinθ + μ’cosθ) = ma です。a = g(sinθ – μ’cosθ) です。

初速 0 なので、変位 x = at²/2 です。
x = v₀²/2g(sinθ + μ’cosθ) となる時の t を求めます。

v₀²/2g(sinθ + μ’cosθ) = g(sinθ – μ’cosθ)t²/2
t² = v₀² /g²(sinθ + μ’cosθ)(sinθ – μ’cosθ)
t = v₀/g√(sinθ + μ’cosθ)(sinθ – μ’cosθ)

v = at
= g(sinθ – μ’cosθ) × v₀/g√(sinθ + μ’cosθ)(sinθ – μ’cosθ)
= v₀√(sinθ – μ’cosθ)/(sinθ + μ’cosθ)

以上より、正解は 3 です。