問 題
ある地域で 1 年間にマグニチュード 7.0 以上の地震が発生する回数を確率変数 X とし、X は、平均 3 のポアソン分布に従うものとする。この地域で1 年間にマグニチュード7.0 以上の地震が少なくとも 1 回発生する確率はいくらか。
なお、平均 λ (λ > 0) のポアソン分布に従う確率変数 Y が、Y = k (k =0、1、2、…) となる確率 P (Y = k) は、
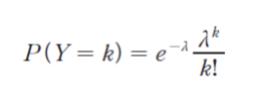
で与えられる。
1. e-3
2. 3e-3
3. 1 -3e-3
4. 1 -2e-3
5. 1 -e-3
正解 (5)
解 説
全く意味がわからなくても、e ≒ 3 とすると選択肢 1,2 は 1/27、1/9 です。「平均 3 回地震が起きる」ような状況で「少なくとも 1 回地震が発生する」のは、確率が大きいと推測できるのではないでしょうか。選択肢 1,2 は誤りと判断できます。当てずっぽうで選ぶ場合であっても、選択肢 3 ~ 5 の中から選べるように具体的に考えましょう!
以下、本問の具体的な解き方 及び 問題文のポアソン分布の式の使い方について説明します。
地震が少なくとも 1 回発生する確率は「1 ー 地震が 1 回も発生しない確率」です。つまり Y = 0 の時の確率を求めて、1 から引けばよいです。問題文の与えられた式に λ = 3、k = 0 を代入します。0! = 1 であることは基礎知識です。
P(Y = 0)
= e-3 30/1
= e-3 です。従って、求める確率は 1 – e-3 です。
以上より、正解は 5 です。

コメント