2022年 国家一般職(デジタル・電気・電子) No.36 解説

　問 題　　　　　

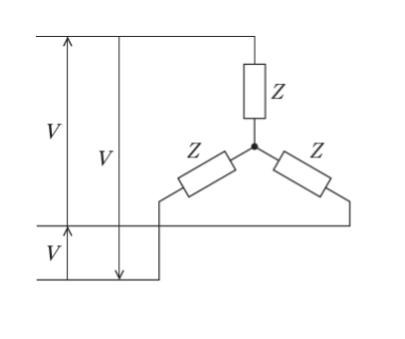
一般に、三相回路全体の電力を三相電力と呼び、各相の電力の和で表される。図のように、三つの線間電圧が V である三相電源に接続された Y 結線負荷において、各相の負荷のインピーダンスの大きさを Z、各相の負荷の力率を cosθ とする。この平衡三相回路の相電圧及び三相電力として最も妥当なのはどれか。　

 

 

 

 

 

　解 説　　　　　

Y 結線や Δ 結線は、三相交流の話です。「電源側と負荷側を考える → Y – Y で考える → １相抜き出して考える」という流れが基本となります。電源側を Y 結線とします。

電源側が Y 結合であれば「線間電圧＝√３ × 相電圧」です。これは基礎知識です。本問では線間電圧が V なので、各相における相電圧は V/√3 です。正解は (1) or (2) です。

電力 P = VI です。これを I を用いず抵抗 R で表現すると、オームの法則 V = RI より、I = V/R とすることで P = V²/R・・・(1) と表すことができます。

三相電力は「各相の相電力 × 3」となります。まず相電力、つまり 1 つの相に注目して電力を考えます。(1) の式の V に相電圧 V/√3 を代入して、P_相 = V²/3R です。

交流における抵抗のようなものが インピーダンス Z です。R を Z に置き換えると P_相 = V²/3Z です。各相における実際の電力 (有効電力) は、力率 cos θ をかけて (V²/3Z) × cos θ です。

従って
三相電力は 3 × (V²/3Z × cos θ) = (V²/Z) × cos θ です。

以上より、正解は 1 です。