問 題

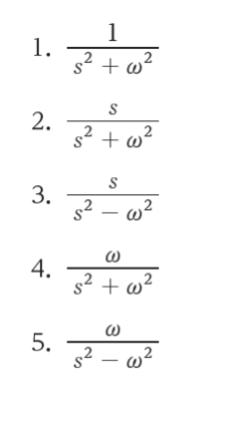
正解 (2)
解 説
H29 no26 の類題です。定義に基づいた積分はとても大変なのですが、今回は「必要であれば…」というヒントがあります。オイラーの公式から cos ωt を eiωt を用いた形で表せば現実的な計算量で解くことができる問題です。また、フーリエ変換の公式として覚えていた場合はすぐに選択肢に飛びついて OK です。
まず、オイラーの公式は「eiθ = cos θ + isin θ」です。問題文に合わせて θ = ωt とします。cos(-θ) = cos θ、sin(-θ) = -sinθ は三角関数の基礎知識です。これらより、cos ωt = 1/2 × (eiωt + e-iωt) と表せます。計算過程は以下の通りです。
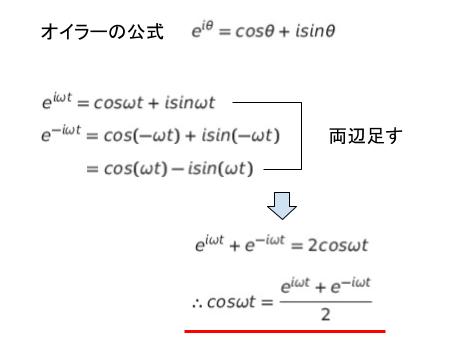
1/2 は外に出して後で掛け算すればよいのでひとまず放置します。ラプラス変換の定義に 代入してみると、∫ dt の内側がそれぞれ
e-st × eiωt = e-(s-iω)t
e-st × e-iωt = e-(s+iω)t
となります。
すると、問題文に与えられたラプラス変換の公式からそれぞれ ∫ e-(s-iω)t → 1/(s-iω) 、∫ e-(s+iω)t → 1/(s+iω) と変換できます!
後は通分して、最後に 1/2 をかければ s/(s2 + ω2) を得ます。1/(s-iω) + 1/(s+iω) の計算過程は以下の通りです。この時点では 最後の 1/2 をかけていないため、分子は 2s となっています。
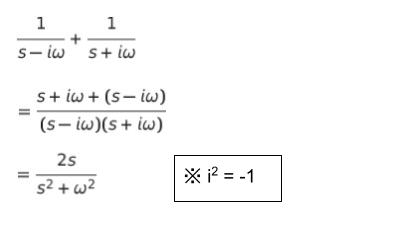
以上より、正解は 2 です。

コメント