2022年 国家一般職(デジタル・電気・電子) No.30 解説

　問 題　　　　　

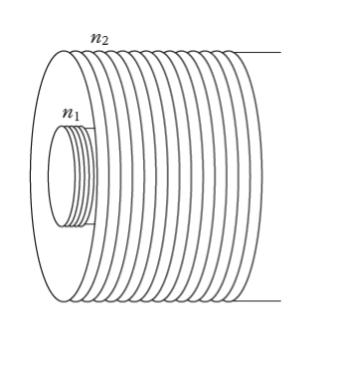
図のような無限に長い同軸ソレノイドにおいて、単位長さ当たりの相互インダクタンスとして最も妥当なのはどれか。

ただし、内側ソレノイドは、断面が断面積 S₁ = 3.0 × 10^-4〔m²〕の円で、単位長さ当たりの巻数 n₁ = 5.0 × 10⁵〔回/m〕であり、外側ソレノイドは、断面が断面積 S₂ = 1.2 × 10^-3〔m²〕の円で、単位長さ当たりの巻数 n₂ = 4.0 × 10⁵〔回/m〕である。また、それぞれのソレノイド内の透磁率 μ₀ = 1.2 × 10^-6〔H/m〕とする。

1．3.6 × 10 H/m
2．7.2 × 10 H/m
3．9.0 × 10 H/m
4．1.8 × 10² H/m
5．2.3 × 10² H/m

 

 

 

 

 

　解 説　　　　　

【相互インダクタンスの求め方】
一方のコイルに電流 i を流す
→ 他方のコイルを貫く磁束 Φ を求める
→ Φ = Mi の M を抜き出す　という流れが基本です。

 

【ソレノイド内部の磁場に関する基礎知識】
・無限長ソレノイドに電流 i を流した際
内部の磁場 H = ni です。※n は単位長あたりの巻数

・環状ソレノイドに電流 i を流した際 (本問 使わない)
内部の磁場 H = Ni/2πr です。※N は全巻数

 

【磁場、磁束密度、磁束の関係　基礎知識】
・磁束密度 B = μH ※μ は透磁率　
・磁束 Φ = BS ※S は断面積
ーーー

内側ソレノイドに電流 i を流した場合を考えます。

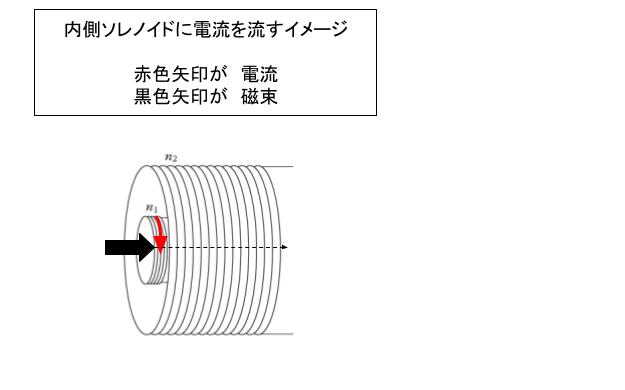
内側のソレノイド内の磁場 H_内 = n_内i_内 ・・・(1) です。

磁束密度 B_内 = μH_内 です。磁束密度 B = μH は基礎知識です。(1) を 代入することで B_内 = μn_内i_内 ・・・(2) と表すことができます。

－－－

視点を外側のソレノイドに移します。内側ソレノイドに電流が流れ、内部に磁束ができたため「外側のソレノイドが貫かれる鎖交磁束 Φ」が生じました。Φ = B_内 × S_内 です。磁束 Φ = BS であることは基礎知識です。(2) を代入することで、Φ = μn_内i_内 × S_内・・・(3) と表せます。

外側のソレノイドを磁束が貫く → コイルは変化を嫌うので電磁誘導が、磁束を弱める方に起きる。 → 電磁誘導における誘導起電力 V について、ファラデーの法則：V = N dΦ/dt が成立するという流れです。

ファラデーの法則の式右辺 Φ に (3) を代入します。本問では「単位長さ当たりの相互インダクタンス」を求めたいので、ファラデーの法則右辺 N には「外側ソレノイドの単位長さ当たりの巻数：n_外」を代入します。

di/dt を端におけば右辺が「n_外 × μn_内 × S_内 (di_内/dt)」です。(di_内/dt) を除いた部分がインダクタンスです。つまり n_外 × μn_内 × S_内 を計算すれば OK です。

n_内 = 5.0 × 10⁵
n_外 = 4.0 × 10⁵
S_内 = 3.0 × 10^-4
μ = 1.2 × 10^-6　を全てかければ 72.0 = 7.2 × 10 です。

以上より、正解は 2 です。