2022年 国家一般職(デジタル・電気・電子) No.29 解説

　問 題　　　　　

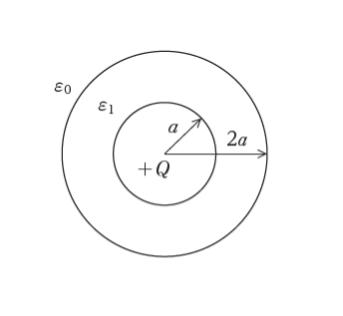
空気中で、図のような半径 a の導体球のまわりを厚さ a の球殻状の誘電率 ε₁ の誘導体で包み、導体球に大きさ Q の電荷を与えた。このとき、無限遠を基準とした導体球の電位として最も妥当なのはどれか。なお、空気中の誘電率は ε₀ とし、ε₁ = 2ε₀ とする。

　

 

 

 

 

 

　解 説　　　　　

電位 V は、電界 E を積分して求めます。電界 E はガウスの法則で求めます。本問では誘電率が異なる領域があるので、場合分けして考えます。

・r > 2a において　ガウスの法則より
∫ E dS = Q/ε₀
4πr²E = Q/ε₀
∴ E = Q/4πr²ε₀

変数 r について ∞ → 2a まで E を積分すれば 基準を∞ とした時の 2a までの V が出せます。定数部分である Q/4πε₀ は後でかければよいです。

∫ 1/r² = -1/r で 「∞ 代入」 ー 「2a 代入」
→ -(-1/2a)
= 1/2a 

・a < r < 2a において ガウスの法則より
∫ E dS = Q/ε₁ = Q/2ε₀
4πr²E = Q/2ε₀ 
∴ E = Q/8πε₀r²

変数 r について 2a → a まで E を積分すれば 基準を 2a とした時の a までの V が出せます。定数部分である Q/8πε₀ は後でかければよいです。

∫ 1/r² = -1/r で 「2a 代入」 ー 「a 代入」
→ – (1/2a – 1/a) 
= 1/2a

∞ → 2a までが V = Q/8aπε₀
2a → a までが V = Q/16aπε₀　なので、足して 3Q/16aπε0

※ 0 < r < a においてガウスの法則を考えれば、閉曲面内の電荷が 0 なので、E = 0 だから V も 0 です。この範囲について考える必要はありません。

以上より、正解は 3 です。

類題 H28 no21 3重同心導体球殻の電界の大きさ
https://yaku-tik.com/koumuin/h28-denjyou-21/